
Modelo de Trabajo Geométrico
Exposición sobre
viernes 21 de septiembre de 2018

Créditos
Exposición sobre el Modelo de Trabajo Geométrico por Sergio Rubio-Pizzorno se distribuye bajo una Licencia Creative Commons Atribución-NoComercial 4.0 Internacional.
Basada en una obra en https://slides.com/zergiorubio/2018-exposicion-cinvestav-matedu .
BY
NC
Hoja de ruta
Metodología del estudio
Problematización de la Geometría
Modelo de Trabajo Geométrico
1
3
2
Metodología "Z" para el estudio de la geometría
"Z" es para indicar que (aún) no tiene nombre.
Pluralista
De emergentes
Sistémica
Indagar en la naturaleza de la geometría relativa a diferentes áreas de conocimiento.
Se espera que entre las distintas naturalezas emerjan puntos en común que entreguen información nueva.
Establecimiento de un modelo que sintetice y articule el aporte de las etapas anteriores.
Etapa pluralista
Epistémica (\(e\))
Epistemológica (\(E\))
Filosófica (\(F\))
Digital (\(D\))
Indagar en la naturaleza de la geometría relativa a diferentes áreas de conocimiento.
A estos conocimientos les denominamos naturalezas, ya que corresponden a aspectos naturales de la geometría, es decir, manera de representarla como un fragmento de la realidad, aunque desde diferentes perspectivas.
\(\vdots\)
Etapa de Emergentes
Todas las naturalezas se refieren al mismo fragmento de la realidad -la geometría-, por lo que se espera que entre las distintas naturalezas emerjan puntos en común que entreguen información nueva.
A continuación, se da cuenta de los aspectos de la naturaleza digital de la geometría que encuentran su fundamento en tales emergentes.
Epistémico-Epistemológico (\(eE\))
Epistemológico-Filosófico (\(EF\))
Epistémico-Filosófico (\(eF\))
Digital (\(D\))
Digital (\(D\))
Digital (\(D\))
Etapa Sistémica
Como ejercicio de articulación y síntesis, se elabora un modelo sobre la geometría sobre qué hacemos y cómo hacemos geometría, el cual toma como base los emergentes para plantear la estructura general del modelo, la cual se complementa con el aporte de las naturalezas para ayudar a describir ciertas cuestiones con más detalle.
Naturalezas
Emergentes
Modelo
Problematización de la geometría
Estudio pluralista, sistémico y progresivo de la geometría, mediante la indagación de sus naturalezas relativas a diferentes esferas de conocimiento.



Epistémica (\(e\))
Epistemológica (\(E\))
Filosófica (\(F\))
Digital (\(D\))
\(eE\)
\(EF\)
\(eF\)
Puntos comunes
Naturalezas
Modelo
Trabajo geométrico considerando el carácter dinámico de la geometría
\(D\)
\(D\)
\(D\)
Pluralista
Emergentes
Sistémico
¿Qué geometría y cómo se aprende ésta en la Era digital?
N. epistémica
N. epistemológica
Asp. epistemológico-filosófico
Importancia del proceso de construcción como generador de invariantes.
En los AGD, los objetos manifiestan propiedades que les son atribuidas a partir de su proceso de construcción y las propiedades teóricas que subyace a la geometría euclidiana (Leung, 2015).
Reconocimiento del carácter dinámico de la geometría, dado por el par transformación-invariante.
El arrastre, el cual puede inducir la noción de transformación geométrica, puesto que se define como una transformación continua en tiempo real (Goldenberg y Cuoco, 1998).
- Construcciones euclidianas.
- Propiedades teóricas y propiedades gráfico-espaciales.
- Estatus de precisión y exactitud de los diagramas geométricos.
Hablar de las Naturalezas




Digital
Asp. epistémico-epistemológico
Asp. epistémico-filosófico
Asp. epistemológico-filosófico
Importancia del proceso de construcción como generador de invariantes.
En los AGD, los objetos manifiestan propiedades que les son atribuidas a partir de su proceso de construcción y las propiedades teóricas que subyace a la geometría euclidiana (Leung, 2015).
Reconocimiento del carácter dinámico de la geometría, dado por el par transformación-invariante.
El arrastre, el cual puede inducir la noción de transformación geométrica, puesto que se define como una transformación continua en tiempo real (Goldenberg y Cuoco, 1998).
Relación dialéctica entre lo concreto y lo teórico.
El arrastre es crucial en la dialéctica entre lo perceptual y lo teórico, propio de todo el razonamiento geométrico (Arzarello y otros, 2002).
Convergencias




Digital
Digital
Digital
Objeto concreto
Objeto teórico
Modelo de Trabajo geométrico
(Rubio-Pizzorno, 2018, pp. 99 - 100)
Relación dialéctica entre lo concreto y lo teórico.
\(eE\)


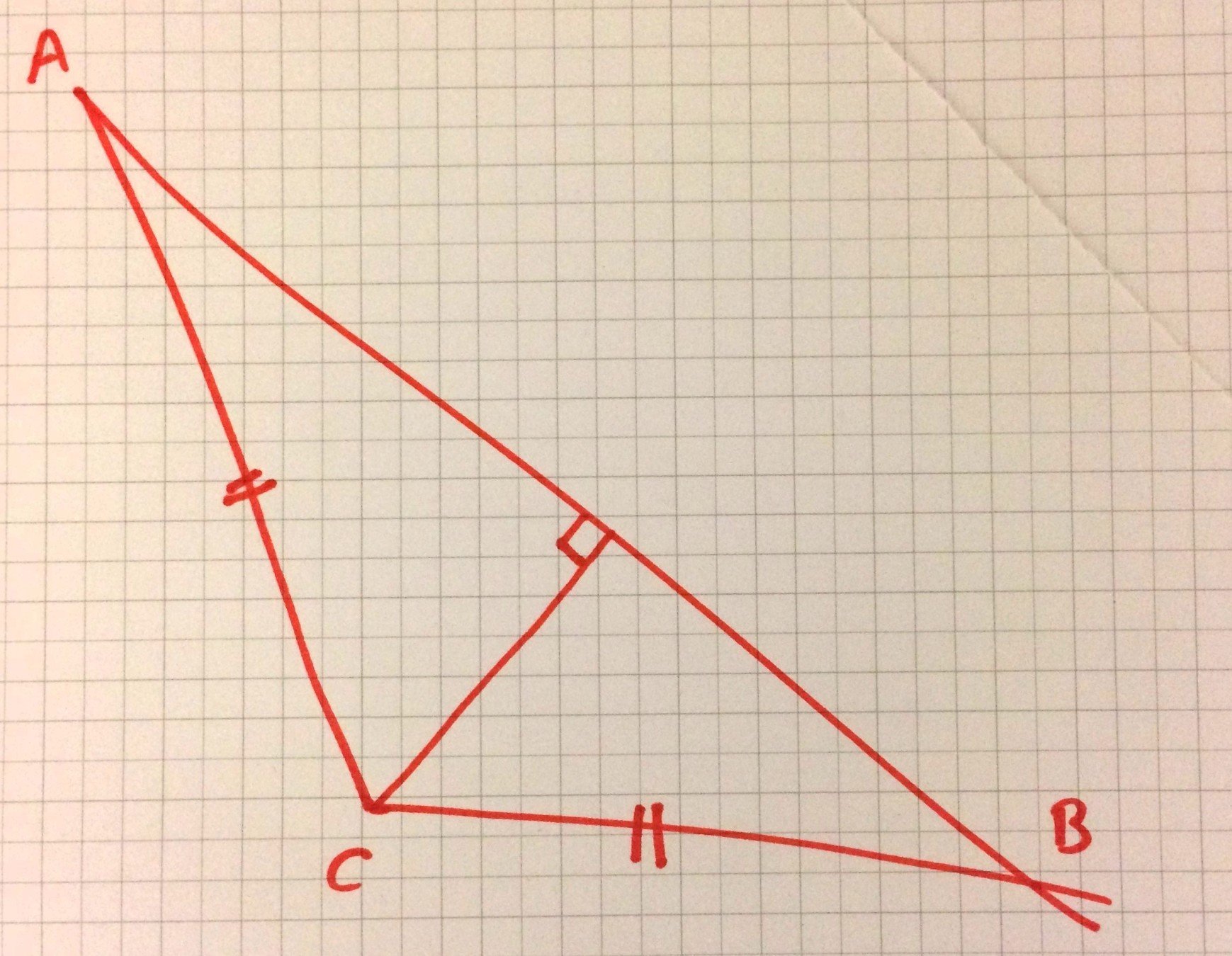

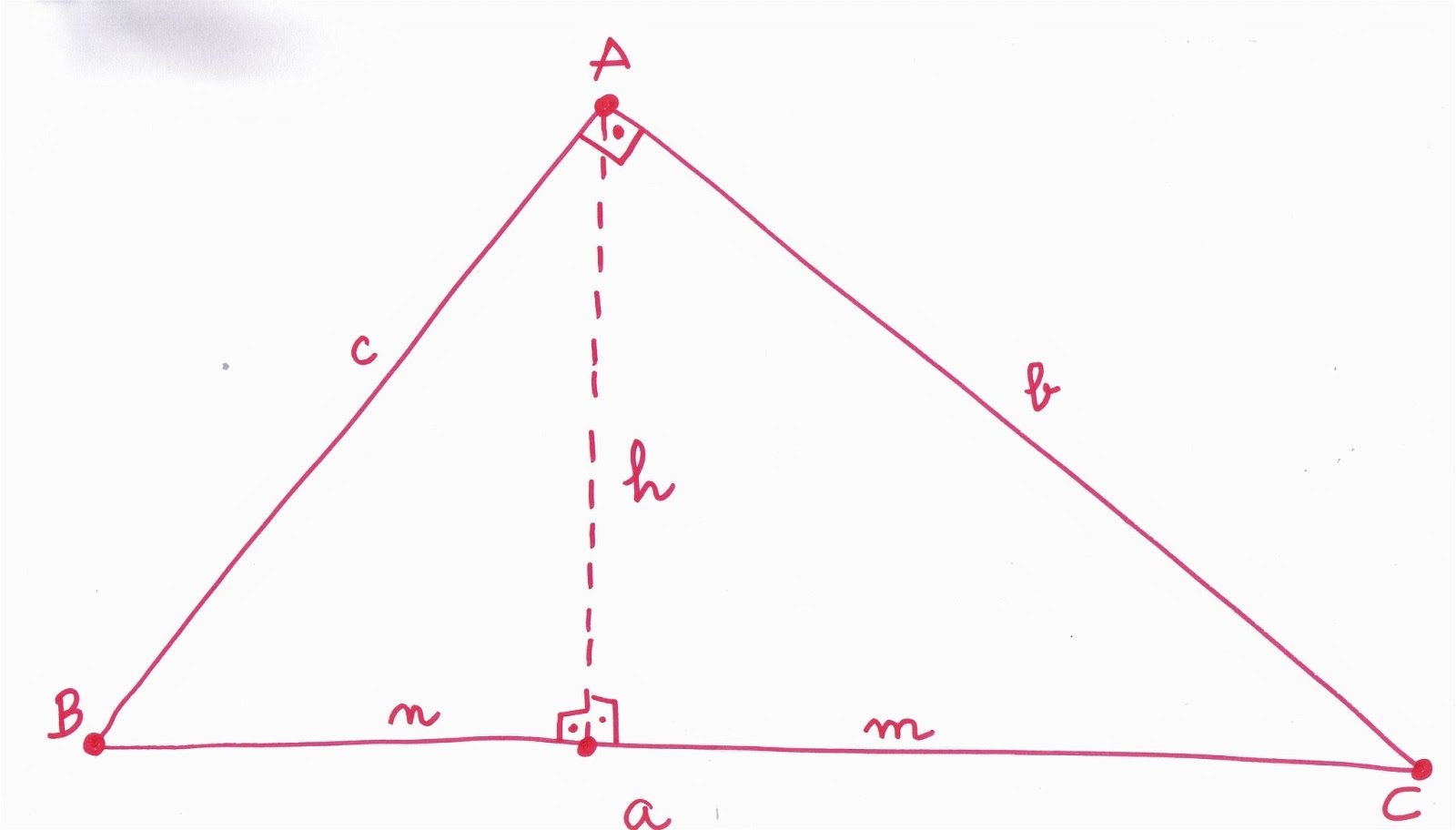
Triángulo


Objeto concreto
Objeto teórico
Representación
(Rubio-Pizzorno, 2018, pp. 100 - 101)
Importancia del proceso de construcción como generador de invariantes.
\(eF\)
\(F\)
Reconocimiento de propiedades geométricas (teóricas) mediante el estudio de diagramas.
Abstracción


Objeto concreto
Objeto teórico
Representación
(Rubio-Pizzorno, 2018, pp. 100 - 101)
\(F\)
Necesidad de una intuición sofisticada, coordinada con una intuición empírica para la identificación de esencias de los diagramas.
Abstracción


Intuición empírica
Intuición sofisticada
Intuición empírica
Intuición sofisticada
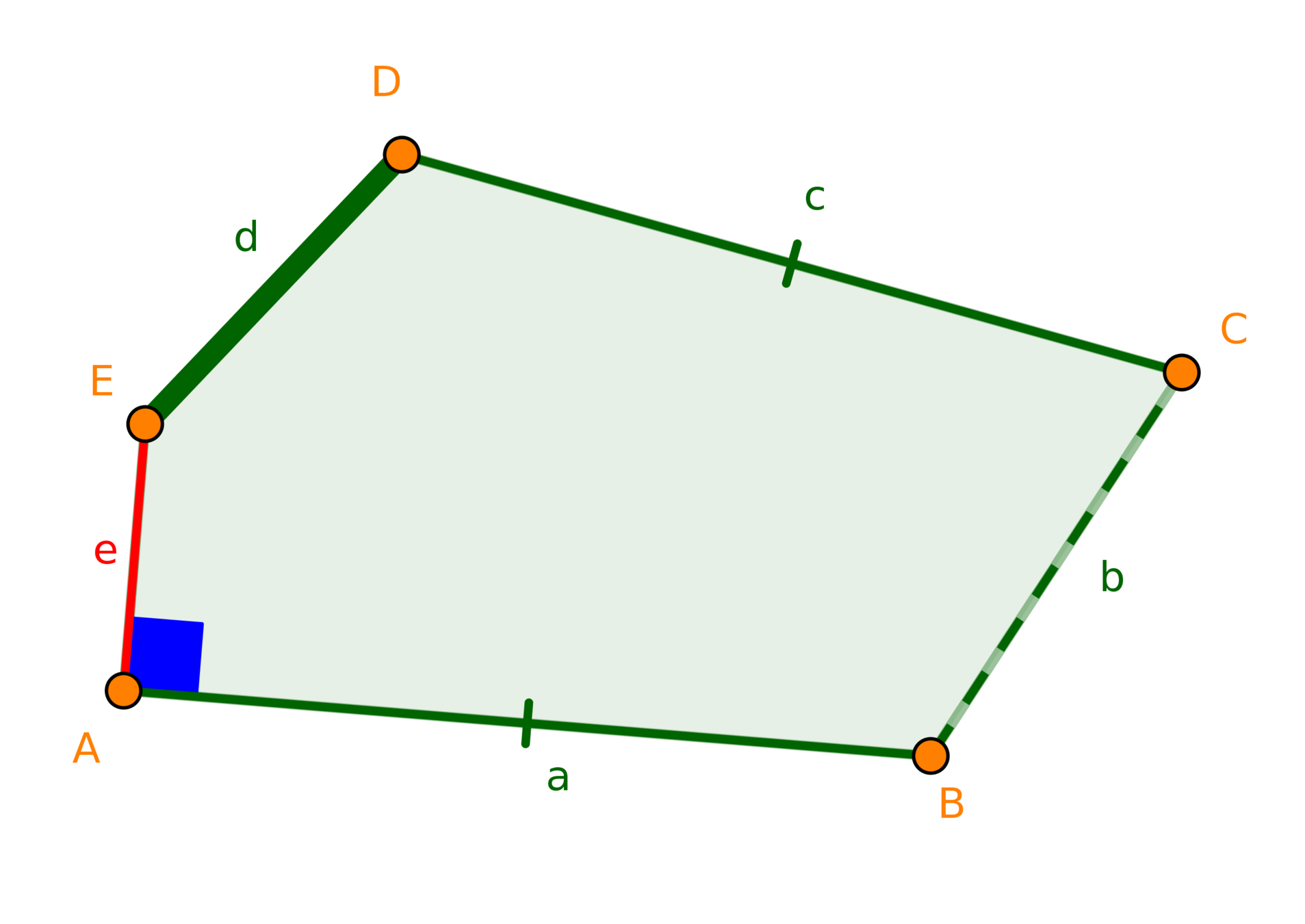
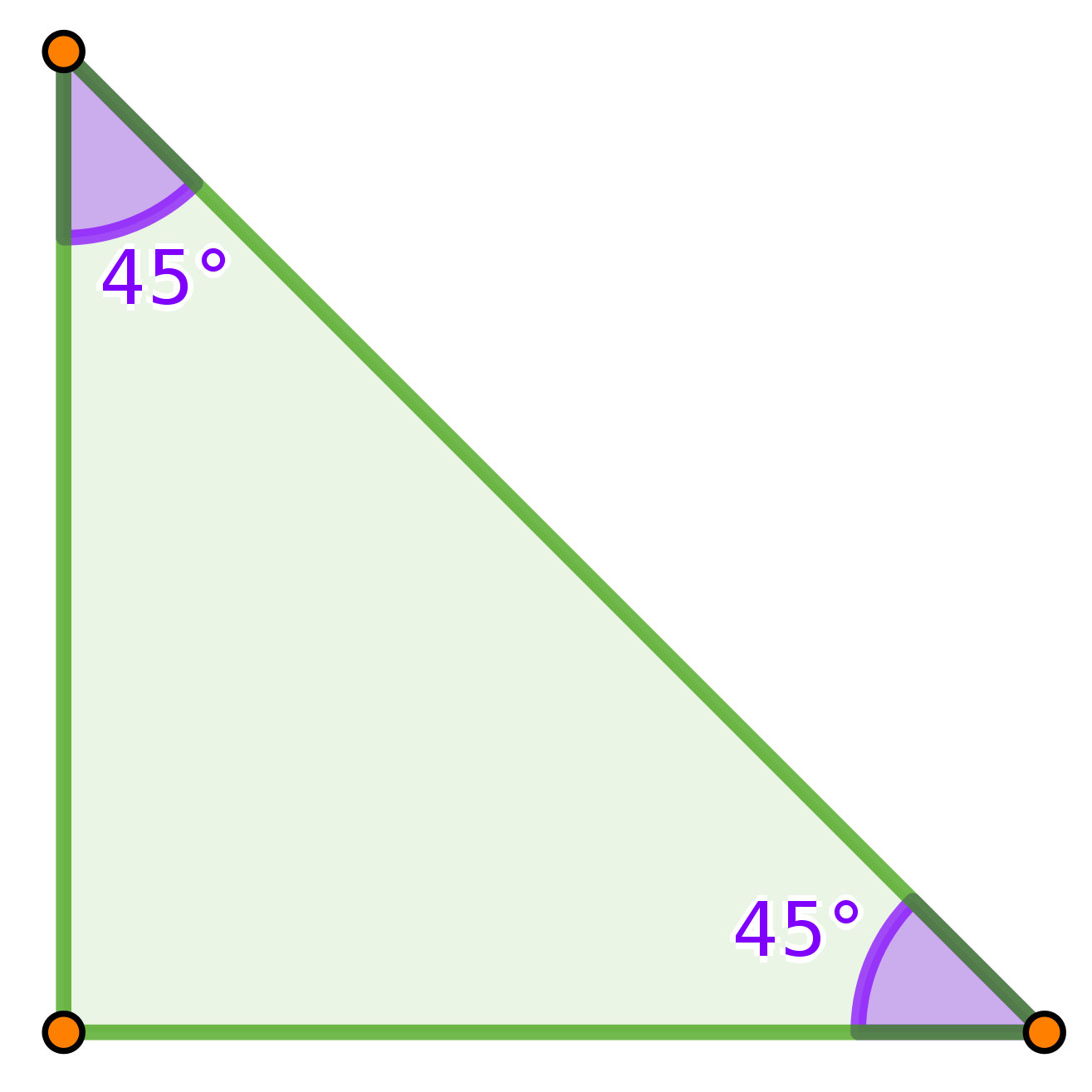
- Grosor.
- Color.
- Línea sólida o punteada.
- Formas.
- Etc.
- Segmento.
- Congruencia.
- Perpendicularidad.
- Paralelismo.
- Etc.
Abstracción
Objeto concreto
Objeto teórico
Representación
(Rubio-Pizzorno, 2018, pp. 100 - 104)
\(F\)
Abstracción


Intuición empírica
Intuición sofisticada
- Interpretación
- Reconocimiento
- Identificación
La intuición sofisticada permite abstraer las propiedades teóricas que los diagramas están representando, ya sea a través de la interpretación de símbolos o el reconocimiento de patrones.
Interpretación
Reconocimiento

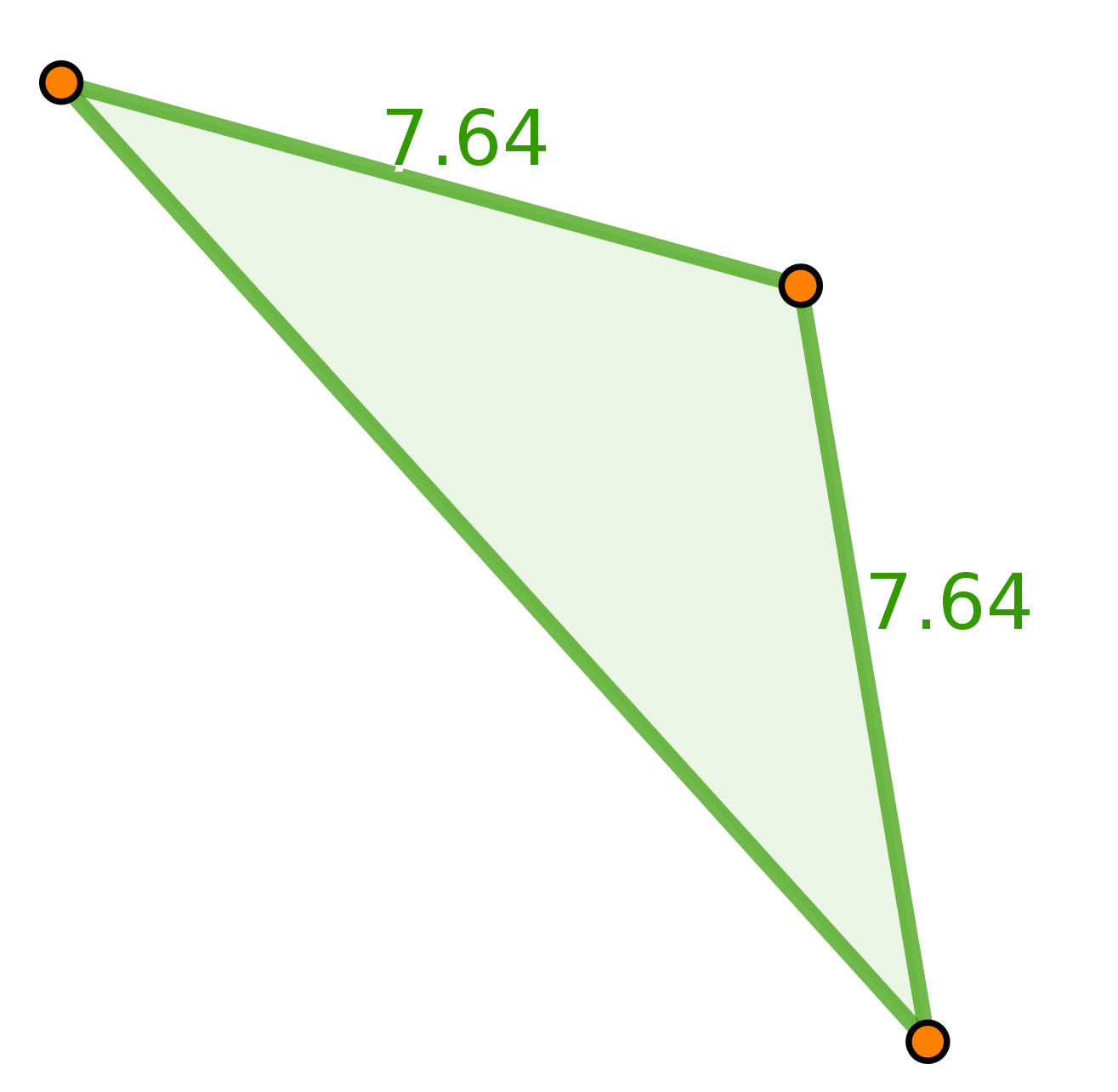


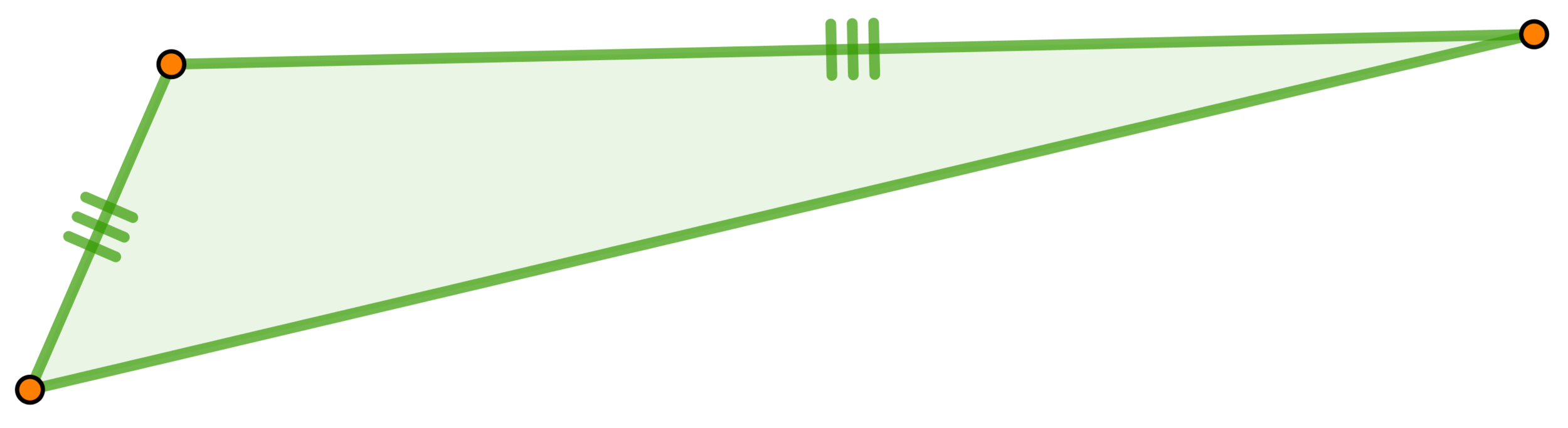
Identificación
Objeto concreto
Objeto teórico
Representación
(Rubio-Pizzorno, 2018, pp. 100 - 101)
\(eF\)
Abstracción


Construcción
Bosquejo
- General
- Particular
Los diagramas pueden manifestar distinto estatus de exactitud y precisión, que lo pueden disponer como un bosquejo, una construcción particular o una construcción general.
Representación
Construcción
Bosquejo
General
Particular
Objeto concreto
Objeto teórico
Representación
(Rubio-Pizzorno, 2018, pp. 67 - 104)
Abstracción


Construcción
Bosquejo
- General
- Particular
Intuición empírica
Intuición sofisticada
- Interpretación
- Reconocimiento
- Identificación
Modelo de Trabajo geométrico
¿PREGUNTAS?
Referencias
Arzarello, F., Olivero, F., Paola, D., y Robutti, O. (2002). A cognitive analysis of dragging practises in Cabri environments. Zentralblatt für Didaktik der Mathematik, 34(3), pp. 66–72. ISSN 1615-679X. doi: 10.1007/BF02655708
Goldenberg, E. Paul y Cuoco, Albert A. (1998). What is Dynamic Geometry? En Richard Lehrer y Daniel Chazan (Eds.), Designing Learning Environments for Developing Understanding of Geometry and Space, pp. 351–367.
Laborde, Colette (2002). Integration of Technology in the Design of Geometry Tasks with Cabri-Geometry. International Journal of Computers for Mathematical Learning, 6(3), pp. 283–317. ISSN 13823892. doi: 10.1023/A:1013309728825
Referencias
Leung, A. (2015). Discernment and Reasoning in Dynamic Geometry Environments. En: Sung Je Cho (Ed.), Selected Regular Lectures from the 12th International Congresson Mathematical Education, pp. 451–469. Springer International Publishing. ISBN: 978-3-319-17186-9. doi: 10.1007/978-3-319-17187-6
Rubio-Pizzorno, S. (2018). Integración digital a la práctica del docente de geometría. Tesis de Maestría no publicada. Ciudad de México, México: Centro de Investigaciones y de Estudios Avanzados (Cinvestav). doi: 10.13140/RG.2.2.15488.94728/1
Rubio-Pizzorno, S. y Montiel, G. (2017). Geometría dinámica como actualización didáctica de la evolución conceptual de la geometría. En P. Perry (Ed.), Encuentro de Geometría y sus Aplicaciones, 23 (pp. 143-148). Bogotá, Colombia: Universidad Pedagógica Nacional. Rescatado de www.encuentrogeometria.com/Documents/2017Memorias.pdf
Referencias
Rubio-Pizzorno, S., Cruz-Márquez, G. y Montiel, G. (en evaluación). Trabajo geométrico, con atención en el carácter dinámico de la goemetría y su proceso de construcción: análisis inicial. En L. A. Serna (Ed.), Acta Latinoamericana de Matemática Educativa, 31. Ciudad de México, México: Comité Latinoamericano de Matemática Educativa. ISSN: 2448-6469.
Rubio-Pizzorno, S.; Farfán-Cera, C. y Montiel, G. (2017). Estrategia de planeación para el trabajo con profesores, integrando tecnología digital. En D. Cobos Sanchiz; E. López-Meneses; A. H. Martín Padilla; L. Molina-García y A. Jaén Martínez (Eds.), INNOVAGOGÍA 2016. III Congreso Internacional sobre Innovación Pedagógica y Praxis Educativa. Libro de Actas. (pp. 1069 - 1077). AFOE Formacion: Sevilla, España. ISBN: 978-84-608-8348-7.
Créditos
Exposición sobre el Modelo de Trabajo Geométrico por Sergio Rubio-Pizzorno se distribuye bajo una Licencia Creative Commons Atribución-NoComercial 4.0 Internacional.
Basada en una obra en https://slides.com/zergiorubio/2018-exposicion-cinvestav-matedu .
BY
NC
Exposición sobre el Modelo de Trabajo Geométrico (Rubio-Pizzorno, 2018) en el Seminario de grupo de la Dra. Gisela Montiel
By Sergio Rubio-Pizzorno
Exposición sobre el Modelo de Trabajo Geométrico (Rubio-Pizzorno, 2018) en el Seminario de grupo de la Dra. Gisela Montiel
[viernes-21-sep-2018] Exposición sobre el Modelo de Trabajo Geométrico (Rubio-Pizzorno, 2018) para el Seminario de grupo de la Dra. Gisela Montiel en Cinvestav. | RESUMEN: El tema de la conferencia es sobre el modelo de Trabajo geométrico, enfatizando en el carácter dinámico de la geometría (Rubio-Pizzorno, 2018). Con base en estos fundamentos teóricos se desarrollan actividades en el ambiente de geometría dinámica de GeoGebra. | REFERENCIA: Rubio-Pizzorno, S. (2018). Integración digital a la práctica del docente de geometría. Tesis de Maestría no publicada. Ciudad de México, México: Centro de Investigaciones y de Estudios Avanzados (Cinvestav). doi: 10.13140/RG.2.2.15488.94728/1
- 1,823








