Generative Adversarial Nets

Cristóbal Silva

Why GANs

  • Simulate Future
  • Work with missing data
  • Multi-modal outputs
  • Realistic generation tasks

Maximum Likelihood

in Deep Learning

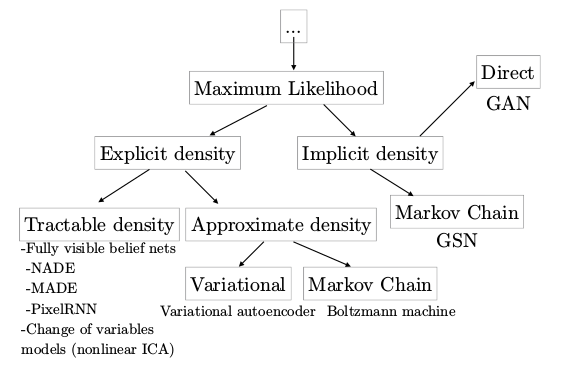
sample without density

GANs

  • Latent code
  • Asymptotically consistent
  • No Markov Chains needed
  • (Subjective) Produces bests samples

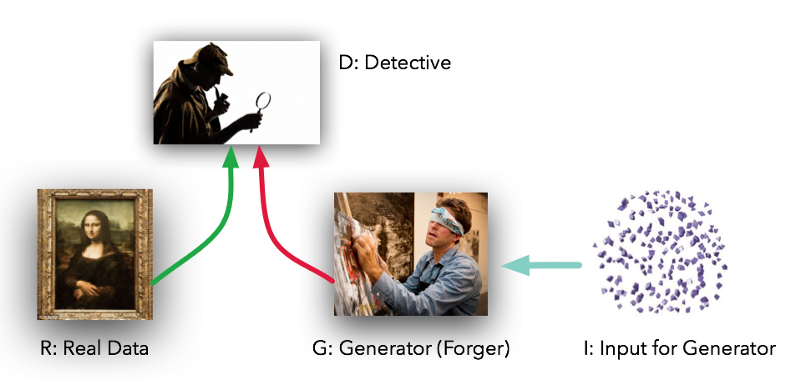
Generator vs Discriminator

Generator vs Discriminator

D(x) = \text{discriminator}
D(x)=discriminatorD(x) = \text{discriminator}
G(z) = \text{generator}
G(z)=generatorG(z) = \text{generator}
z = \text{noise input}
z=noise inputz = \text{noise input}
X = \text{training data}
X=training dataX = \text{training data}
p_{generator}(x)
pgenerator(x)p_{generator}(x)
p_{data}(x)
pdata(x)p_{data}(x)
0: real

1: fake

Nash Equilibrium

p_{data}(x) = p_{generator}(x)
pdata(x)=pgenerator(x)p_{data}(x) = p_{generator}(x)
D(x) = \frac{1}{2}
D(x)=12D(x) = \frac{1}{2}

In other words, discriminator can't discriminate

Loss Function

Minimax Game

J^{(D)} = -\frac{1}{2}\mathbb{E}_{\mathbf{x}\sim p_{data}} \log{D(\mathbf{x})} - \frac{1}{2}\mathbb{E}_{\mathbf{z}} \log{(1 - D(G(\mathbf{z}))}
J(D)=−12Ex∼pdatalogD(x)−12Ezlog(1−D(G(z))J^{(D)} = -\frac{1}{2}\mathbb{E}_{\mathbf{x}\sim p_{data}} \log{D(\mathbf{x})} - \frac{1}{2}\mathbb{E}_{\mathbf{z}} \log{(1 - D(G(\mathbf{z}))}
J^{(G)} = -J^{(D)}
J(G)=−J(D)J^{(G)} = -J^{(D)}

Non-Saturating Game

J^{(D)} = -\frac{1}{2}\mathbb{E}_{\mathbf{x}\sim p_{data}} \log{D(\mathbf{x})} - \frac{1}{2}\mathbb{E}_{\mathbf{z}} \log{(1 - D(G(\mathbf{z}))}
J(D)=−12Ex∼pdatalogD(x)−12Ezlog(1−D(G(z))J^{(D)} = -\frac{1}{2}\mathbb{E}_{\mathbf{x}\sim p_{data}} \log{D(\mathbf{x})} - \frac{1}{2}\mathbb{E}_{\mathbf{z}} \log{(1 - D(G(\mathbf{z}))}
J^{(G)} = -\frac{1}{2}\mathbb{E}_{\mathbf{z}} \log{D(G(\mathbf{z}))}
J(G)=−12EzlogD(G(z))J^{(G)} = -\frac{1}{2}\mathbb{E}_{\mathbf{z}} \log{D(G(\mathbf{z}))}

Vanishing gradient

GANs + PyTorch,

Let's model and sample from a Gaussian!

import torch
import torch.nn as nn
import torch.nn.functional as F
import torch.optim as optim

PyTorch is a new DL framework based on dynamic graphs

Comes with high level API for network design

No static-graph required, easier to debug

What we need

Input data

Input noise

our ground truth

our latent code

def real_distribution_sampler(mu, sigma, n):
    samples = np.random.normal(mu, sigma, (1, n))
    return torch.Tensor(samples)
def noise_distribution_sampler(m, n):
    return torch.rand(m, n)

Generator

class Generator(nn.Module):
    def __init__(self):
        super().__init__()
        self.fc1 = nn.Linear(1, 100)
        self.fc2 = nn.Linear(100, 100)
        self.fc3 = nn.Linear(100, 1)
    
    def forward(self, x):
        x = F.elu(self.fc1(x))
        x = F.sigmoid(self.fc2(x))
        x = self.fc3(x)
        return x
class Discriminator(nn.Module):
    def __init__(self):
        super().__init__()
        self.fc1 = nn.Linear(100, 50)
        self.fc2 = nn.Linear(50, 50)
        self.fc3 = nn.Linear(50, 1)
    
    def forward(self, x):
        x = F.elu(self.fc1(x))
        x = F.elu(self.fc2(x))
        x = F.sigmoid(self.fc3(x))
        return x

Discriminator

1

100

100

1

100

1

50

50

Training

Parameters

Optimization

n_epochs = 30000

# binary cross entropy loss
criterion = nn.BCELoss()

# discriminator params
D = Discriminator()
d_steps = 1
d_optimizer = optim.SGD(
               D.parameters(), 
               lr=2e-4
              )


# generator params
G = Generator()
g_steps = 1
g_optimizer = optim.SGD(
               G.parameters(), 
               lr=2e-4
              )
batch_size = 100

for epoch in range(n_epochs)
    for i in range(d_steps):
        D.zero_grad()
        # train D on real data
        d_real_data   = Variable(real_distribution_sampler(mu, sigma, 100))
        d_real_output = D(d_real_data)
        d_real_loss   = criterion(d_real_output, Variable(torch.ones(1)))
        d_real_loss.backward()  # compute/store gradients, but don't update

        # train D on fake data
        d_gen_input   = Variable(noise_distribution_sampler(batch_size, 1))
        d_fake_data   = G(d_gen_input).detach()  # important to avoid training G
        d_fake_output = D(d_fake_data.t())
        d_fake_loss   = criterion(d_fake_output, Variable(torch.zeros(1)))
        d_fake_loss.backward()
        
        d_optimizer.step()

    for j in range(g_steps):
        # train G based on D output
        G.zero_grad()
        g_gen_input   = Variable(noise_distribution_sampler(batch_size, 1))
        g_fake_data   = G(g_gen_input)
        g_fake_output = D(g_fake_data.t())
        g_fake_loss   = criterion(g_fake_output, Variable(torch.ones(1)))
        g_fake_loss.backward()
        g_optimizer.step()

Experiment

mean 4.00
var 1.25

SGD

Results 1

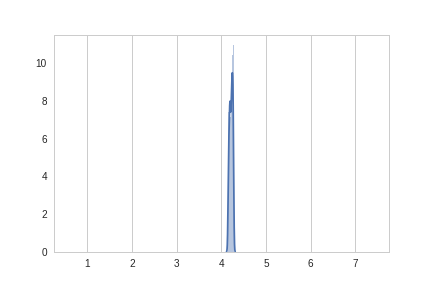
mean 4.00
var 1.25
mean 4.21
var 0.03

... the dreaded mode-collapse!

SGD

Results 2

mean 4.00
var 1.25
mean 3.82
var 1.13

SGD with Momentum

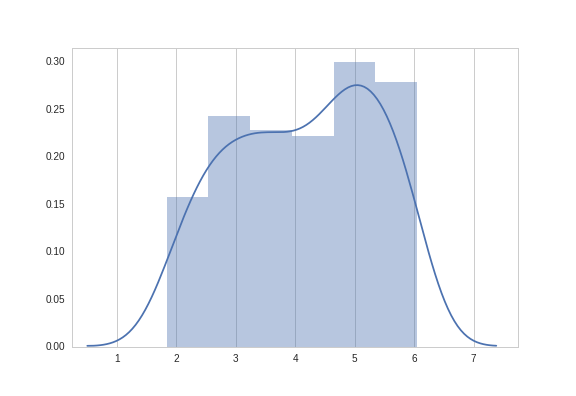
Results 3

mean 4.00
var 1.25
mean 4.26
var 1.09

ADAM

GAN Zoo

What we saw was 2 years ago, what now?

Many, many GANs

ose-GAN



enderGAN

AD-GAN

riple-GAN

nrolled GAN

AE-GAN

aterGAN
A

B

C

D

E

F

G

H

I

J

K

L

M
N

O

P

Q

R

S

T

U

V

W

X

Y

Z
daGAN

ayesian GAN

atGAN

CGAN

BGAN

-GAN

eneGAN

yperGAN

GAN





AGAN

cGAN

 

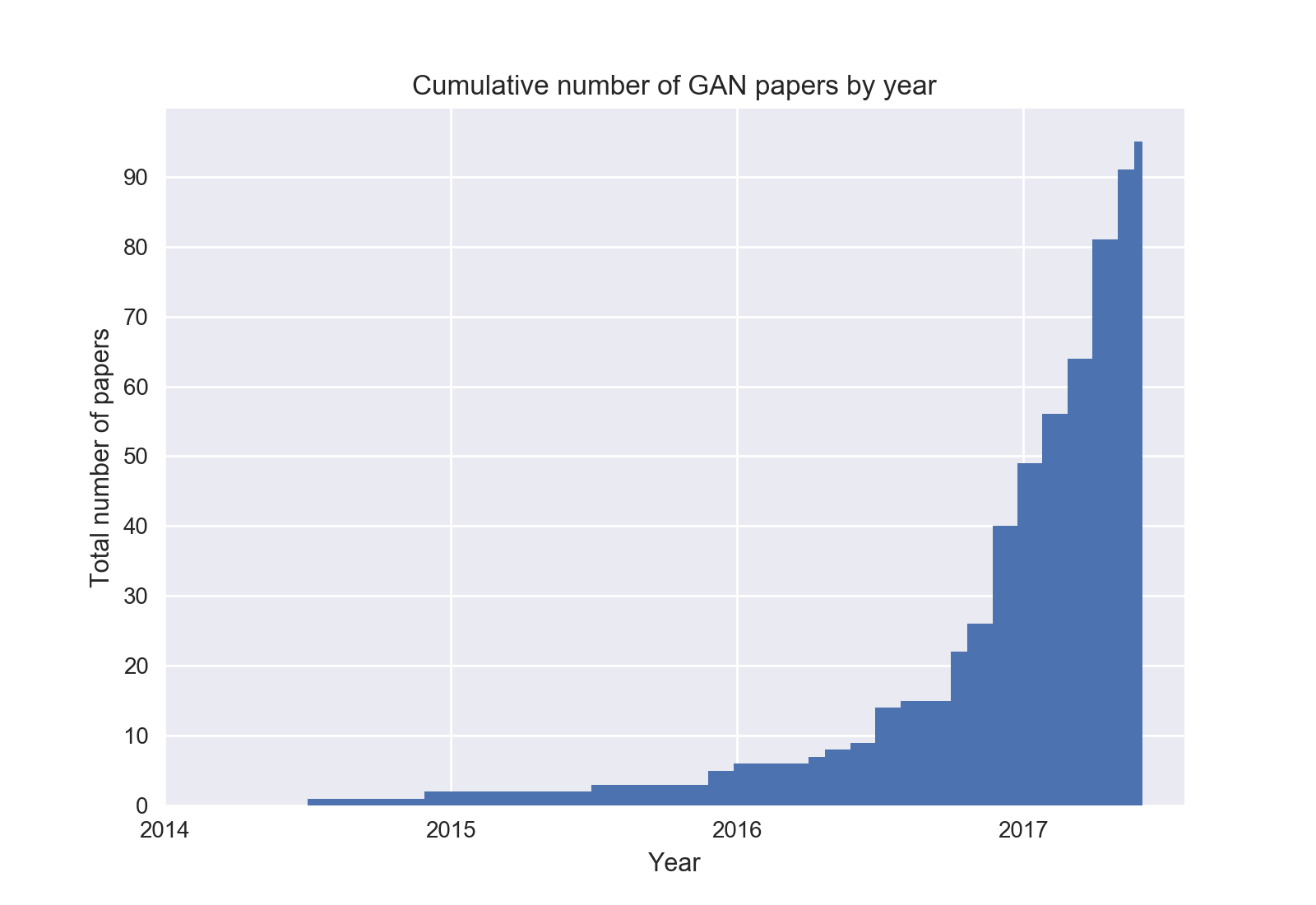
More than 90 papers in 2017

DCGAN

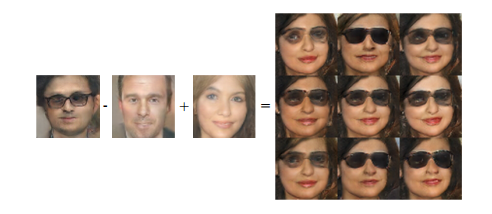
GANs can encode concepts

pix2pix

DiscoGAN

Cycle-GANs

Problems

  • Classical GANs generate from input noise. This means you can't select the features you want the sample to have
  • If you wanted to generate a picture with specific features, there's no way of determining which initial noise values would produce that picture, other than searching over the entire distribution.

Generative Adversarial Nets

By crsilva

Made with Slides.com

Generative Adversarial Nets

  • 594

More from crsilva