Cluster-size decay in kernel-based spatial random graphs
Júlia Komjáthy
joint with Joost Jorritsma, Dieter Mitsche
Random Discrete Structures
March 2023
Papers: tiny.cc/cluster-size-ksrg
Cluster-size decay in supercrit. nearest-neighbor percolation
\mathbb{P}\big(k\le |\mathcal{C}(0)|<\infty\big)=
\exp\big(-\Theta(k^{\mathbf{\zeta}})\big),\qquad\zeta=\frac{d-1}d
[Grimmett & Marstrand '90, Kesten & Zhang '90]
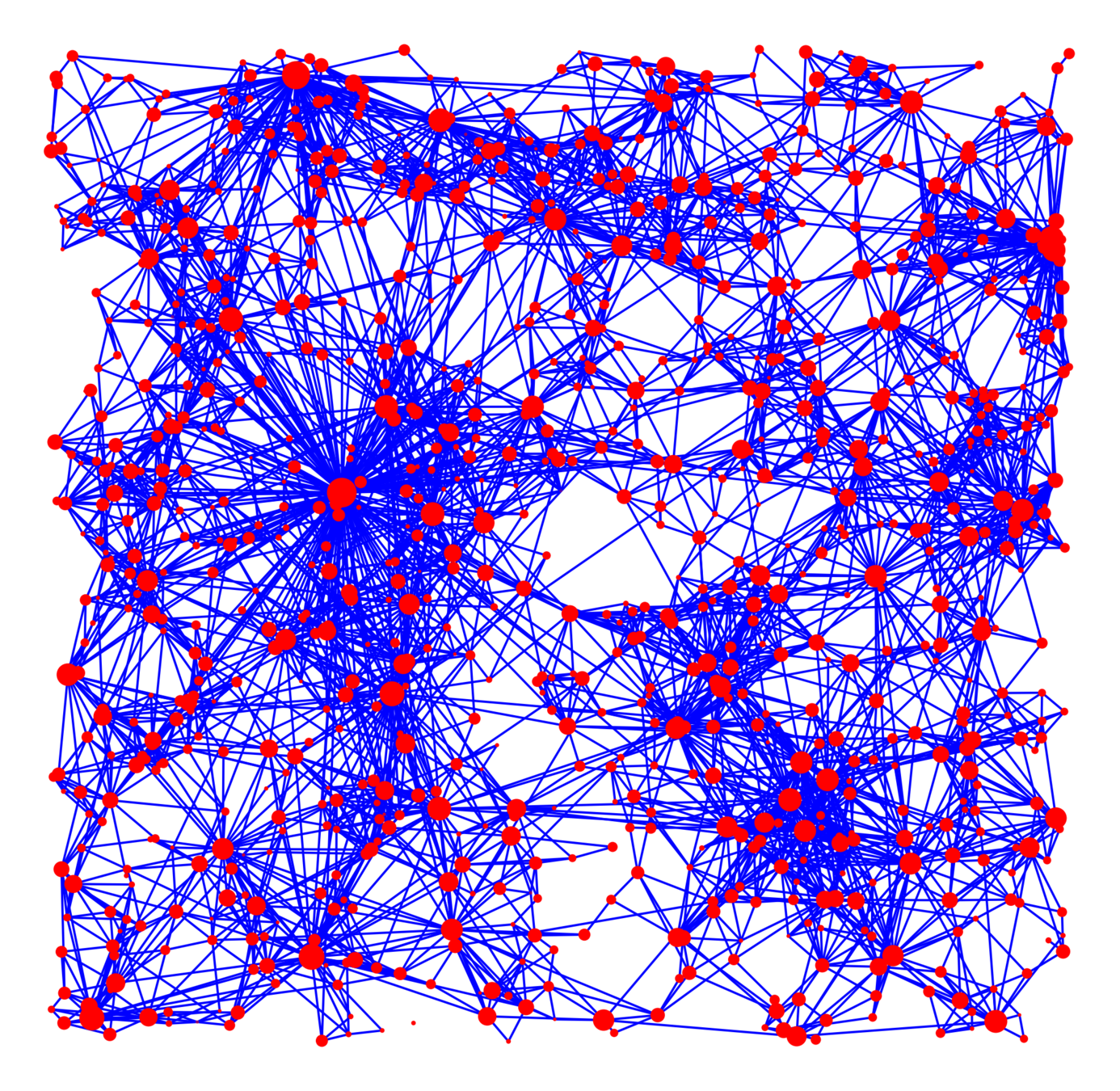
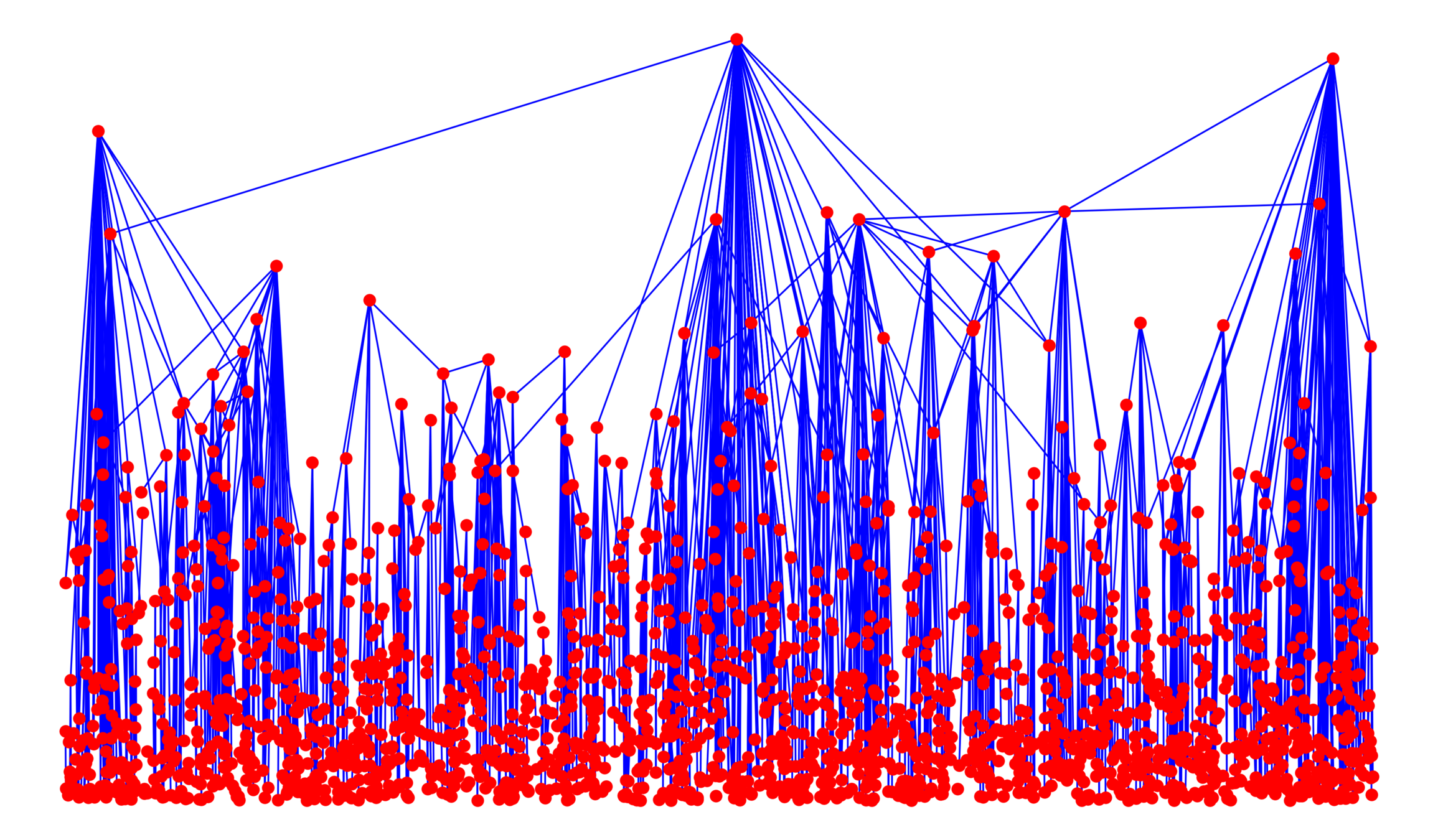
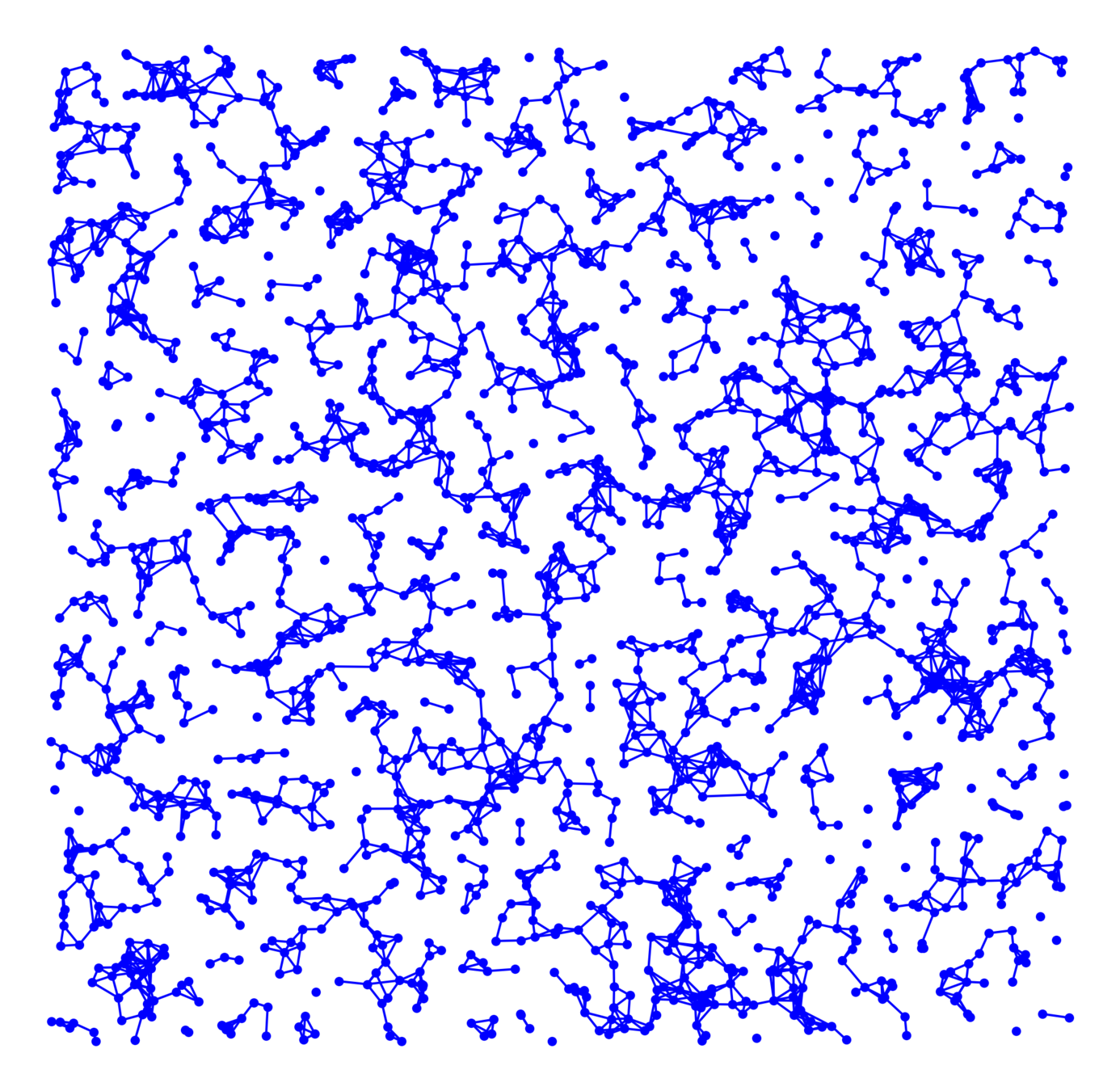
Hyperbolic random graph
Scale-free percolation
Long-range percolation
Age-dependent RCM
Random geom. graph
Nearest-neighbor percolation
Kernel-based spatial random graphs
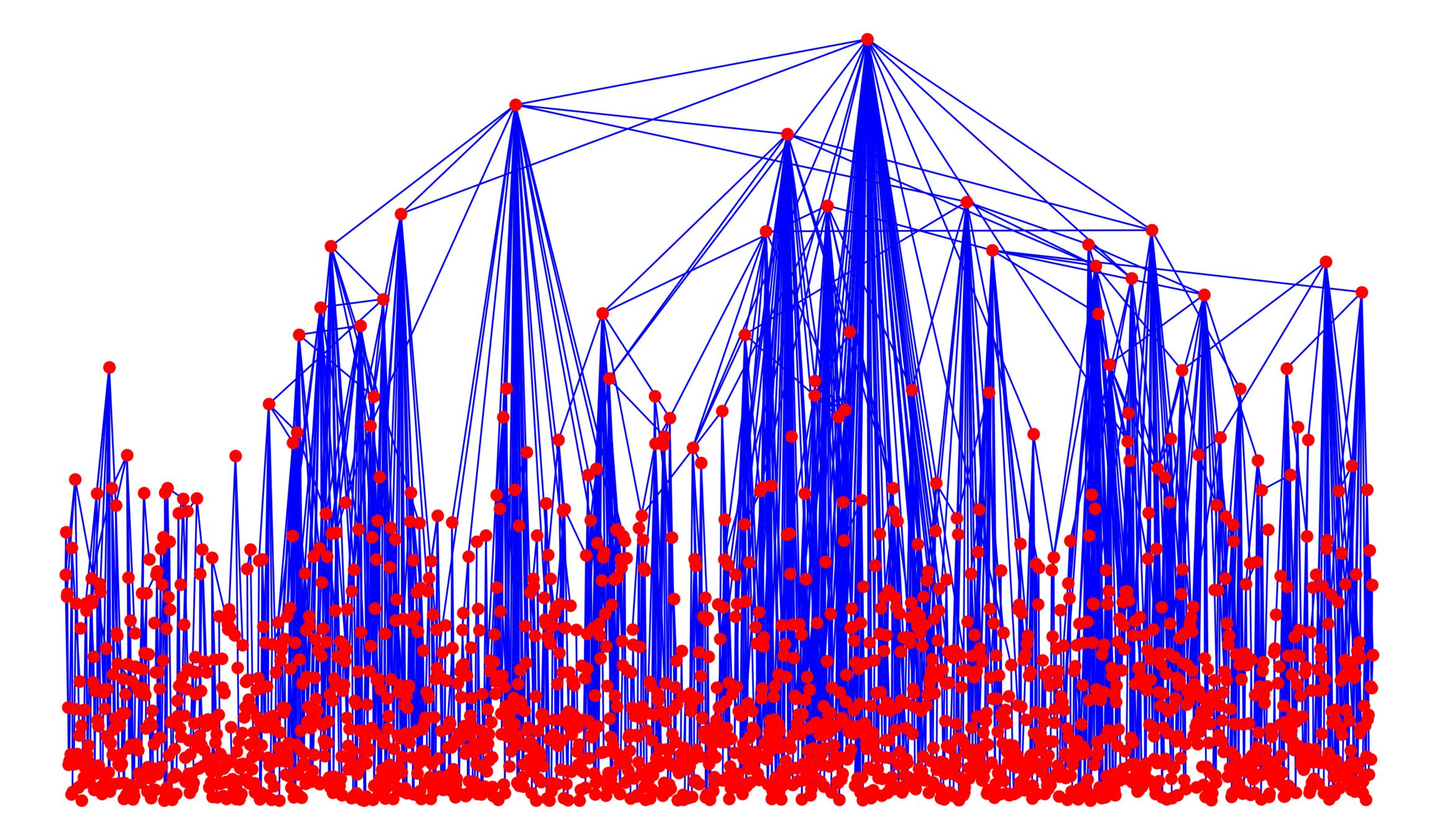
Vertex set \(\mathcal{V}_\infty\)
- Spatial locations \(x_v\in\mathbb{R}^d\): PPP(1) or \(\mathbb{Z}^d\),
- i.i.d. weights \(w_v\ge 1\): \(\mathbb{P}(w_v\ge w)=w^{-(\tau-1)}\),
Edge set \(\mathcal{E}_\infty\)
- Symmetric kernel \(\kappa(w_u, w_v)\),
- Long-range parameter \(\alpha>1\),
- Edge-density \(\beta>0\),
Connection probability
$$\mathbb{P}\big(u\leftrightarrow v\mid \mathcal{V}_\infty\big)=\bigg(\beta\frac{\kappa(w_u, w_v)}{\|x_u-x_v\|^d}\bigg)^\alpha\wedge 1$$
Vertex set \(\mathcal{V}_\infty\)
- Spatial locations \(x_v\in\mathbb{R}^d\): PPP(1) or \(\mathbb{Z}^d\),
- i.i.d. weights \(w_v\ge 1\): \(\mathbb{P}(w_v\ge w)=w^{-(\tau-1)}\),
$$\mathbb{P}\big(u\leftrightarrow v\mid \mathcal{V}_\infty\big)=\bigg(\beta\frac{\kappa(w_u, w_v)}{\|x_u-x_v\|^d}\bigg)^\alpha$$
$$\mathbb{P}\big(u\leftrightarrow v\mid \mathcal{V}_\infty\big)=\phantom{\bigg(\beta}\frac{\kappa(w_u, w_v)}{\phantom{\|x_u-x_v\|^d}}\phantom{\bigg)^\alpha\wedge 1}$$
$$\mathbb{P}\big(u\leftrightarrow v\mid \mathcal{V}_\infty\big)=\phantom{\bigg(\beta}\frac{\kappa(w_u, w_v)}{\|x_u-x_v\|^d}\phantom{\bigg)^\alpha\wedge 1}$$
$$\mathbb{P}\big(u\leftrightarrow v\mid \mathcal{V}_\infty\big)=\bigg(\phantom{\beta}\frac{\kappa(w_u, w_v)}{\|x_u-x_v\|^d}\bigg)^\alpha\phantom{\wedge 1}$$
$$\mathbb{P}\big(u\leftrightarrow v\mid \mathcal{V}_\infty\big)$$
Kernel-based spatial random graphs
Vertex set \(\mathcal{V}_\infty\)
- Spatial locations \(x_v\in\mathbb{R}^d\): PPP(1),
- i.i.d. weights \(w_v\ge 1\): Pareto(\(\tau\)),
Edge set \(\mathcal{E}_\infty\)
- Symmetric kernel \(\kappa(w_1, w_2)\),
- Edge-density \(\beta>0\),
- Long-range parameter \(\alpha>1\),
Connection probability
$$\mathbb{P}\big(u\leftrightarrow v\mid \mathcal{V}_\infty\big)=\bigg(\beta\frac{\kappa(w_u, w_v)}{\|x_u-x_v\|^d}\bigg)^\alpha\wedge 1$$
Vertex set \(\mathcal{V}_\infty\)
- Spatial locations \(x_v\in\mathbb{R}^d\): PPP(1), or \(\mathbb{Z}^d\),
- i.i.d. weights \(w_v\ge 1\): \(\mathbb{P}(w_v\ge w)=w^{-(\tau-1)}\),
Edge set \(\mathcal{E}_\infty\)
- Symmetric kernel \(\kappa(w_1, w_2)\),
- Edge-density \(\beta>0\),
- Long-range parameter \(\alpha>1\),
The interpolating kernel
Connection probability
$${\color{grey}\mathbb{P}\big(u\leftrightarrow v\mid \mathcal{V}_\infty\big)=\bigg(\beta}\frac{\kappa(w_u, w_v)}{\color{grey}\|x_u-x_v\|^d}{\color{grey}\bigg)^\alpha\wedge 1}$$
A parameterized kernel: \(\sigma\ge 0\)
$$\kappa_{\sigma}(w_u, w_v):=\max\{w_u, w_v\}\min\{w_u, w_v\}^\sigma$$
- \(\tau: \mathbb{P}(w_v\ge w)=w^{-(\tau-1)}.\)
- \(\sigma\): assortativity
- \(\sigma\): interpolation
\frac{\sigma}{\tau-1}
\frac1{\tau-1}
1
1
\sigma=\tau-1
\tau=2
\sigma=1
\sigma=1
\sigma=\tau-2
\sigma=\tau-2
\sigma=0
\sigma=0
SFP/GIRG
Hyperbolic RG
Age-dep. RCM
Scale-free Gilbert
Long-range percolation
Random geom. graph
Nearest-neighbor percolation
Degree distribution
\frac{\sigma}{\tau-1}
\frac1{\tau-1}
1
1
\sigma=\tau-1
\tau=2
\sigma=1
\sigma=\tau-2
\sigma=0
\tau_\mathrm{deg}=\tau
\tau_\mathrm{deg}=\tfrac{\sigma+1}{\sigma-(\tau-2)}
\mathrm{deg}(0)=\infty
Theorem. When \(\tau>2\):
Theorem. When \(\tau<2\):
- Infinite degrees
- Bounded diameter
$$\mathbb{P}(\mathrm{deg}(0)\ge k)\sim k^{-(\tau_\mathrm{deg}-1)}.$$
[Deijfen, v.d. Hofstad, Hooghiemstra '13]
[Gracar, Grauer, Lüchtrath, Mörters '18]
[Heydenreich, Hulshof, Jorritsma '17]
[Hirsch '17]
[v.d. Hofstad, v.d. Hoorn, Maitra, '22]
[Jorritsma, K., Mitsche, '23]
[Lüchtrath '22]
Theorem. When \(\tau<2\):
Theorem. When \(\tau>2\):
$${\color{grey}\mathbb{P}(\mathrm{deg}(0)\ge k)\sim k^{-(\tau_\mathrm{deg}-1)}.}$$
Small components in supercritical setting
- Largest component \(\mathcal{C}_n^{(1)}\):
- Component of the origin \(\mathcal{C}(0)\): $$\mathbb{P}\big(k\le |\mathcal{C}(0)|<\infty\big)= $$
- Second-largest component: $$|\mathcal{C}_n^{(2)}|=\Theta\big(\phantom{what}\big)$$
Questions
\frac{|\mathcal{C}_n^{(1)}|}{n}\overset{\mathbb{P}}\longrightarrow
\mathbb{P}\Big(|\mathcal{C}_n^{(1)}|\le (1-\varepsilon)\mathbb{E}\big[|\mathcal{C}_n^{(1)}|\big]\Big)=
Some known results about \(\zeta\)
- Speed of lower tail of large deviation:$$\mathbb{P}\big(|\mathcal{C}_n^{(1)}|\le (1-\varepsilon)\mathbb{E}\big[|\mathcal{C}_n^{(1)}|\big]\big)=\exp\big(-\Theta(n^\zeta)\big)$$where \(|\mathcal{C}_n^{(1)}|=\Theta_\mathbb{P}(n)\).
- Cluster-size decay: $$\mathbb{P}\big(k\le |\mathcal{C}(0)|<\infty\big)= \exp\big(-\Theta(k^{\mathbf{\zeta}})\big);$$
- Second-largest component: $$|\mathcal{C}_n^{(2)}|=\Theta\big((\log(n))^{1/\zeta}\big).$$
\zeta=\frac{d-1}d
|\mathcal{C}_n^{(2)}|=\mathcal{O}\big((\log(n))^{??}\big)
|\mathcal{C}_n^{(2)}|=\Theta\big((\log(n))^{2/(3-\tau)}\big)
[Alexander & Chayes & Chayes '90, Grimmett (& Marstrand),
Kesten & Zhang '90,
...,
Lichev, Lodewijks, Mitsche, Schapira '22,
Penrose '05]
[Sly & Crawford'12]
[Kiwi & Mitsche '17]
When \(\tau>2\), there exists \(\zeta\in(0,1)\) s.t.
Supercritical scaling exponent \(\zeta\)
- Speed of lower tail of large deviation:
where \(|\mathcal{C}_n^{(1)}|=\Theta_\mathbb{P}(n)\). - Cluster-size decay: $$\mathbb{P}\big(k\le |\mathcal{C}(0)|<\infty\big)= \exp\big(-\Theta(k^{\mathbf{\zeta}})\big);$$
- Second-largest component: $$|\mathcal{C}_n^{(2)}|=\Theta\big((\log(n))^{1/\zeta}\big).$$
When \(\tau>2\), there exists \(\zeta\in(0,1)\) s.t.
\frac{\sigma}{\tau-1}
\frac1{\tau-1}
1
1
\sigma=\tau-1
\tau=2
\zeta_\mathrm{nn}:=\frac{d-1}{d}
\zeta_\mathrm{hh}:=\frac{\sigma+2-\tau}{2-(\tau-1)/\alpha}
\zeta_\mathrm{lh}:=\frac{\tau-1}{\alpha}-(\tau-2)
\zeta_\mathrm{ll}:=2-\alpha
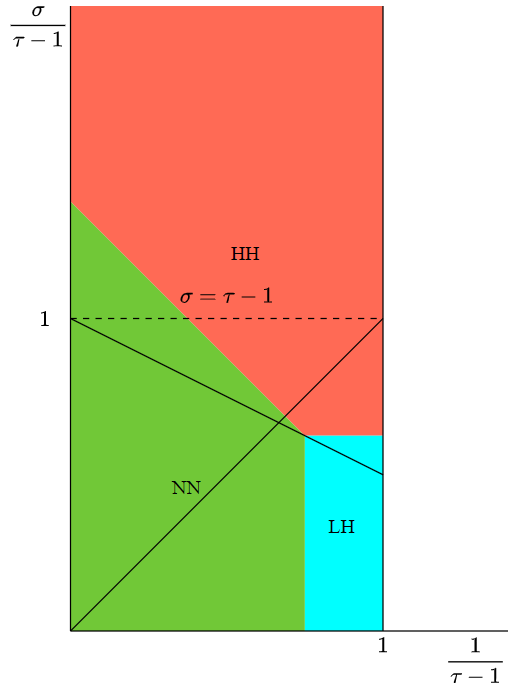
Only four possible values
\mathbb{P}\big(|\mathcal{C}_n^{(1)}|\le (1-\varepsilon)\mathbb{E}\big[|\mathcal{C}_n^{(1)}|\big]\big)=\exp\big(-\Theta(n^\zeta)\big)
Phase diagram of \(\zeta\)
\zeta=\max\{\zeta_\mathrm{ll}, \zeta_\mathrm{lh}, \zeta_\mathrm{hh}, \zeta_\mathrm{nn}\}
- Speed of lower tail of large deviation:
where \(|\mathcal{C}_n^{(1)}|=\Theta_\mathbb{P}(n)\). - Cluster-size decay: $$\mathbb{P}\big(k\le |\mathcal{C}(0)|<\infty\big)= \exp\big(-\Theta(k^{\mathbf{\zeta}})\big);$$
- Second-largest component: $$|\mathcal{C}_n^{(2)}|=\Theta\big((\log(n))^{1/\zeta}\big).$$
When \(\tau>2\), there exists \(\zeta\in(0,1)\) s.t.
\mathbb{P}\big(|\mathcal{C}_n^{(1)}|\le (1-\varepsilon)\mathbb{E}\big[|\mathcal{C}_n^{(1)}|\big]\big)=\exp\big(-\Theta(n^\zeta)\big)
\zeta_\mathrm{nn}:=\frac{d-1}{d}
\zeta_\mathrm{hh}:=\frac{\sigma+2-\tau}{2-(\tau-1)/\alpha}
\zeta_\mathrm{lh}:=\frac{\tau-1}{\alpha}-(\tau-2)
\zeta_\mathrm{ll}:=2-\alpha
Only four possible values
Conjecture "almost" proven [JKM'23]
\(d=1\): \(\qquad\zeta_\mathrm{nn}>\max\{\zeta_\mathrm{ll}, \zeta_\mathrm{lh}, \zeta_\mathrm{hh}\}\quad \Longrightarrow\quad \)subcritical
[Gracar, Mönch, Lüchtrath '22]
Consider supercritical interpolating model, \(\sigma\le\tau-1\).
- Speed of lower tail of large deviation:
- Law of large numbers
- Cluster-size decay: $$\mathbb{P}\big(k\le |\mathcal{C}(0)|<\infty\big)\sim \exp\big(-\Theta(k^{\max(Z)})\big);$$
- Second-largest component: $$|\mathcal{C}_n^{(2)}|\sim\Theta\big((\log(n))^{1/\max(Z)}\big).$$
If \(\zeta_\mathrm{nn}\) is not the unique maximum of \(Z:=\{\zeta_\mathrm{ll}, \zeta_\mathrm{lh}, \zeta_\mathrm{hh}, \zeta_\mathrm{nn}\}\):
\mathbb{P}\big(|\mathcal{C}_n^{(1)}|\le (1-\varepsilon)\mathbb{E}\big[|\mathcal{C}_n^{(1)}|\big]\big)=\exp\big(-\Theta(n^\zeta)\big);
\frac{|\mathcal{C}_n^{(1)}|}{n}\overset{\mathbb{P}}\longrightarrow
\mathbb{P}\big(\mathcal{C}(0)=\infty\big);
Long-range percolation for nn-regime [JKM'23]
If \(\zeta_\mathrm{nn}\) is the unique maximum of \(Z\), \(d>1\):
- Always lower bound;
- Upper bound: no weights, high edge-density \(\beta\gg\beta_c\).
Gap: Monotonicity of \(\zeta\)
$$d=2\\\alpha=1.6$$
Proof strategy: 4 steps
\mathbb{P}\big(k\le |\mathcal{C}(0)|<\infty\big) \le \exp\big(-A'k^\zeta\big)
\Longrightarrow
|\mathcal{C}_n^{(2)}|\ge A(\log n)^{1/\zeta}
\Longrightarrow
(2)
(4)
\mathbb{P}\big(|\mathcal{C}_n^{(2)}|\ge k\big)\le n\exp\big(-Ak^\zeta\big)
\mathbb{P}\big(k\le |\mathcal{C}(0)|<\infty\big) \ge \exp\big(-A'k^\zeta\big)
(1)
(3)
Lower bounds
Upper bounds
Lower bounds: an isolated component
Aim: Find minimal \(\zeta\) s.t.
\mathbb{P}\big(k \le |\mathcal{C}(0)|<\infty\big)\ge\exp\big(-Ak^\zeta\big);
Isolation events
- \(\mathcal{C}(0)\ge k\) in \(\Theta(k)\)-volume box,
-
\(\Theta(k)\)-volume box disconnected:
- Empty boundary
- High-weight vertices are dangerous
- Especially close to boundary
- No edges
- Trade-off \(\gamma\)
k^{1/d}
2k^{1/d}
0
Lower bounds: an isolated component
Aim: Find minimal \(\zeta\) s.t.
\mathbb{P}\big(k \le |\mathcal{C}(0)|<\infty\big)\ge\exp\big(-Ak^\zeta\big);
Isolation costs (vertices)
\mathbb{P}(\text{empty yellow})=\phantom{\exp\big(-k^{(d-1)/d}\big)}
k^{(d-1)/d}
\mathbb{E}[|\text{boundary}|]\sim k^{(d-1)/d}
\mathbb{E}[|\text{other yellow}|]\sim
k^{1-\gamma(\tau-1)}
k^{1/d}
2k^{1/d}
0
\mathbb{P}(\text{empty yellow})=\exp\big(-\mathbb{E}[|\text{yellow}|]\big)
\mathbb{E}[|\text{boundary}|]\sim
\Longrightarrow \quad \zeta\ge\max\big\{\tfrac{d-1}{d}, 1-\gamma(\tau-1)\big\}
\mathbb{P}(W\ge w)=w^{-(\tau-1)}
Lower bounds: an isolated component
Aim: Find minimal \(\zeta\) s.t.
\mathbb{P}\big(k \le |\mathcal{C}(0)|<\infty\big)\ge\exp\big(-Ak^\zeta\big);
Isolation costs (edges)
k^{(d-1)/d}
\mathbb{P}(\text{no edges})\sim\exp\big(-\mathbb{E}[|\text{red}\leftrightarrow\text{blue}|])
\zeta\ge\max\big\{\tfrac{d-1}{d}, 1-\gamma(\tau-1)\big\}.
\begin{aligned}
\mathbb{E}[|\text{red}\leftrightarrow\text{blue}|]&\sim \max_{0\le\gamma_1\le\gamma_2\le\gamma}\mathbb{E}[|k^{\gamma_1}\text{-vert.}|] \cdot\mathbb{E}[|k^{\gamma_2}\text{-vert.}|]\\
&\hspace{50pt}\cdot q\big((0, k^{\gamma_1}), (k, k^{\gamma_2})\big)
\end{aligned}
\begin{aligned}
\mathbb{E}[|\text{red}\leftrightarrow\text{blue}|]&\sim
\end{aligned}
\begin{aligned}\Longrightarrow \quad\zeta\ge
\max_{0\le\gamma_1\le\gamma_2\le\gamma}
\{2-\alpha&+\gamma_1(\sigma\alpha-(\tau-1))\\&+ \gamma_2(\alpha-(\tau-1))\}\end{aligned}
\begin{aligned}\Longrightarrow \quad\zeta\ge
\max_{\phantom{0\le\gamma_1\le\gamma_2\le\gamma}}
\{\phantom{2-\alpha}&\phantom{+\gamma_1(\sigma\alpha-(\tau-1))}\\&\phantom{+ \gamma_2(\alpha-(\tau-1))}\}\end{aligned}
Isolation costs (edges)
\begin{aligned}\zeta\ge
\max_{0\le\gamma_1\le\gamma_2\le\gamma}
\{2-\alpha&+\gamma_1(\sigma\alpha-(\tau-1))\\&+ \gamma_2(\alpha-(\tau-1))\}\end{aligned}
Possible optimizers
(\gamma_1^\star, \gamma_2^\star)\in\big\{
(0, 0),
\phantom{(0, \gamma),
(\gamma, \gamma)}
\big\}
(\gamma_1^\star, \gamma_2^\star)\in\big\{
(0, 0),
(0, \gamma),
\phantom{(\gamma, \gamma)}
\big\}
(\gamma_1^\star, \gamma_2^\star)\in\big\{
(0, 0),
(0, \gamma),
(\gamma, \gamma)
\big\}
(\gamma_1^\star, \gamma_2^\star)\in\big\{
\phantom{(0, 0),
(0, \gamma),
(\gamma, \gamma)}
\big\}
\begin{aligned}\zeta\ge
\max
\{&\phantom{2-\alpha,}\\
&\phantom{2-\alpha + \gamma(\alpha-(\tau-1)),}\\
&\phantom{2-\alpha + \gamma((\sigma+1)-2(\tau-1))}\}
\end{aligned}
\begin{aligned}\zeta\ge
\max
\{&2-\alpha,\\
&\phantom{2-\alpha + \gamma(\alpha-(\tau-1)),}\\
&\phantom{2-\alpha + \gamma((\sigma+1)-2(\tau-1))}\}
\end{aligned}
\begin{aligned}\zeta\ge
\max
\{&2-\alpha,\\
&2-\alpha + \gamma(\alpha-(\tau-1)),\\
&\phantom{2-\alpha + \gamma((\sigma+1)-2(\tau-1))}\}
\end{aligned}
\begin{aligned}\zeta\ge
\max
\{&2-\alpha,\\
&2-\alpha + \gamma(\alpha-(\tau-1)),\\
&2-\alpha + \gamma((\sigma+1)-2(\tau-1))\}
\end{aligned}
Minimizing \(\zeta\)
\begin{aligned}\zeta=\min_\gamma
\max
\{&2-\alpha,\\
&2-\alpha + \gamma(\alpha-(\tau-1)),\\
&2-\alpha + \gamma((\sigma+1)-2(\tau-1)),\\
&1-\gamma(\tau-1),
\\
&\tfrac{d-1}d
\}
\end{aligned}
Edges, vertices
Aim: Find minimal \(\zeta\) s.t.
\mathbb{P}\big(k \le |\mathcal{C}(0)|<\infty\big)\ge\exp\big(-Ak^\zeta\big);
Lower bound wrap-up
Conclusion:
\begin{aligned}\zeta=
\max
\{&\zeta_\mathrm{ll}, \zeta_\mathrm{lh}, \zeta_\mathrm{hh}, \zeta_\mathrm{nn}
\}
\end{aligned}
Aim: Find minimal \(\zeta\) s.t.
\mathbb{P}\big(k \le |\mathcal{C}(0)|<\infty\big)\ge\exp\big(-Ak^\zeta\big);
nn
ll
lh
hh
\begin{aligned}\zeta=
\max
\{&\phantom{\zeta_\mathrm{ll}, \zeta_\mathrm{lh}, \zeta_\mathrm{hh}, \zeta_\mathrm{nn}}
\}
\end{aligned}
\begin{aligned}\zeta=
\max
\{&\zeta_\mathrm{ll}, \phantom{\zeta_\mathrm{lh}, \zeta_\mathrm{hh}, \zeta_\mathrm{nn}}
\}
\end{aligned}
\begin{aligned}\zeta=
\max
\{&\zeta_\mathrm{ll}, \zeta_\mathrm{lh}, \phantom{\zeta_\mathrm{hh}, \zeta_\mathrm{nn}}
\}
\end{aligned}
\begin{aligned}\zeta=
\max
\{&\zeta_\mathrm{ll}, \zeta_\mathrm{lh}, \zeta_\mathrm{hh}, \phantom{\zeta_\mathrm{nn}}
\}
\end{aligned}
Thank you!
Consider supercritical interpolating model, \(\sigma\le\tau-1\).
- Speed of lower tail of large deviation:
- Law of large numbers
- Cluster-size decay: $$\mathbb{P}\big(k\le |\mathcal{C}(0)|<\infty\big)\sim \exp\big(-\Theta(k^{\max(Z)})\big);$$
- Second-largest component: $$|\mathcal{C}_n^{(2)}|\sim\Theta\big((\log(n))^{1/\max(Z)}\big).$$
If \(\zeta_\mathrm{nn}\) is not the unique maximum of \(Z:=\{\zeta_\mathrm{ll}, \zeta_\mathrm{lh}, \zeta_\mathrm{hh}, \zeta_\mathrm{nn}\}\):
\mathbb{P}\big(|\mathcal{C}_n^{(1)}|\le (1-\varepsilon)\mathbb{E}\big[|\mathcal{C}_n^{(1)}|\big]\big)=\exp\big(-\Theta(n^\zeta)\big);
\frac{|\mathcal{C}_n^{(1)}|}{n}\overset{\mathbb{P}}\longrightarrow
\mathbb{P}\big(\mathcal{C}(0)=\infty\big);
Upper bound: second-largest component
Reveal graph in stages.
-
Form "backbone"
with "\((k^{\gamma_1}, k^{\gamma_2})\)"-edges of length \(k^{1/d}\). - Merge all large components with backbone with edges of length \(k^{1/d}\).
k^{1/d}
2k^{1/d}
0
k^{1/d}
2k^{1/d}
0
k^{1/d}
2k^{1/d}
0
Three techniques: \(\zeta_\mathrm{ll}, \zeta_\mathrm{lh}\), and \(\zeta_\mathrm{hh}\):
No control short edges/local geometry:
no upper bound (nn)
Prevent too large components
Consider supercritical interpolating model, \(\sigma\le\tau-1\).
If \(\zeta_\mathrm{nn}\) is not the unique maximum of \(Z:=\{\zeta_\mathrm{ll}, \zeta_\mathrm{lh}, \zeta_\mathrm{hh}, \zeta_\mathrm{nn}\}\)
- Cluster-size decay: $$\mathbb{P}\big(k\le |\mathcal{C}(0)|<\infty\big)\sim \exp\big(-\Theta(k^{\max(Z)})\big);$$
- Second-largest component: $$|\mathcal{C}_n^{(2)}|\sim\Theta\big((\log(n))^{1/\max(Z)}\big).$$
If \(\zeta_\mathrm{nn}\) is the unique maximum of \(Z\), \(d>1\):
- Always lower bound;
- Upper bound: no weights, high edge-density \(\beta\gg\beta_c\).
\(\zeta_\mathrm{ll}=2-\alpha, \qquad \zeta_\mathrm{lh}=\frac{\tau-1}{\alpha}-(\tau-2), \qquad \zeta_\mathrm{hh}=\frac{3-\tau}{2-(\tau-1)/\alpha}, \qquad \zeta_\mathrm{nn}=\frac{d-1}d\)
Upper bounds
Aim: Maximize \(\zeta\) s.t.
\mathbb{P}\big(|\mathcal{C}_n^{(2)}|\ge k\big)\lesssim n\exp\big(-k^\zeta\big).
\mathbb{P}\big(|\mathcal{C}_n(0)\ge k, 0\notin\mathcal{C}_n^{(1)}\big)\le\mathbb{P}\big(|\mathcal{C}_n^{(2)}|\ge k\big)\lesssim\exp(-\tfrac12k^\zeta)
When \(n\le\exp\big(-\tfrac12k^{\zeta}\big)\)
When \(k=k_n=(2\log(n))^{1/\zeta}\)
\mathbb{P}\big(|\mathcal{C}_n^{(2)}|\ge (2\log(n))^{1/\zeta}\big)\lesssim n\exp\big(-2\log(n)\big).
Upper bound: second-largest component
Reveal graph in stages.
-
Form "backbone"
with "\((k^{\gamma_1}, k^{\gamma_2})\)"-edges of length \(k^{1/d}\). - Merge all large components with backbone.
k^{1/d}
2k^{1/d}
0
k^{1/d}
2k^{1/d}
0
k^{1/d}
2k^{1/d}
0
Three techniques: \(\zeta_\mathrm{ll}, \zeta_\mathrm{lh}\), and \(\zeta_\mathrm{hh}\):
No control short edges/local geometry:
no upper bound (nn)
Lower bounds: an isolated component
Aim: Find minimal \(\zeta\) s.t.
\mathbb{P}\big(k \le |\mathcal{C}(0)|<\infty\big)\ge\exp\big(-Ak^\zeta\big);
Isolation costs (edges)
k^{(d-1)/d}
\mathbb{P}(\text{no edges})\sim\exp\big(-\mathbb{E}[|\text{red}\leftrightarrow\text{blue}|])
\zeta\ge\max\big\{\tfrac{d-1}{d}, 1-\gamma(\tau-1)\big\}.
\begin{aligned}
\mathbb{E}[|\text{red}\leftrightarrow\text{blue}|]&\sim \max_{0\le\gamma_1\le\gamma_2\le\gamma}\mathbb{E}[|k^{\gamma_1}\text{-vert.}|] \cdot\mathbb{E}[|k^{\gamma_2}\text{-vert.}|]\\
&\hspace{50pt}\cdot q\big((0, k^{\gamma_1}), (k, k^{\gamma_2})\big)
\end{aligned}
\begin{aligned}
\mathbb{E}[|\text{red}\leftrightarrow\text{blue}|]&\sim
\end{aligned}
\begin{aligned}\Longrightarrow \quad\zeta\ge
\max_{0\le\gamma_1\le\gamma_2\le\gamma}
\{2-\alpha&+\gamma_1(\sigma\alpha-(\tau-1))\\&+ \gamma_2(\alpha-(\tau-1))\}\end{aligned}
\begin{aligned}\Longrightarrow \quad\zeta\ge
\max_{\phantom{0\le\gamma_1\le\gamma_2\le\gamma}}
\{\phantom{2-\alpha}&\phantom{+\gamma_1(\sigma\alpha-(\tau-1))}\\&\phantom{+ \gamma_2(\alpha-(\tau-1))}\}\end{aligned}
Isolation costs (edges)
\begin{aligned}\zeta\ge
\max_{0\le\gamma_1\le\gamma_2\le\gamma}
\{2-\alpha&+\gamma_1(\sigma\alpha-(\tau-1))\\&+ \gamma_2(\alpha-(\tau-1))\}\end{aligned}
Possible optimizers
(\gamma_1^\star, \gamma_2^\star)\in\big\{
(0, 0),
\phantom{(0, \gamma),
(\gamma, \gamma)}
\big\}
(\gamma_1^\star, \gamma_2^\star)\in\big\{
(0, 0),
(0, \gamma),
\phantom{(\gamma, \gamma)}
\big\}
(\gamma_1^\star, \gamma_2^\star)\in\big\{
(0, 0),
(0, \gamma),
(\gamma, \gamma)
\big\}
(\gamma_1^\star, \gamma_2^\star)\in\big\{
\phantom{(0, 0),
(0, \gamma),
(\gamma, \gamma)}
\big\}
\begin{aligned}\zeta\ge
\max
\{&\phantom{2-\alpha,}\\
&\phantom{2-\alpha + \gamma(\alpha-(\tau-1)),}\\
&\phantom{2-\alpha + \gamma((\sigma+1)-2(\tau-1))}\}
\end{aligned}
\begin{aligned}\zeta\ge
\max
\{&2-\alpha,\\
&\phantom{2-\alpha + \gamma(\alpha-(\tau-1)),}\\
&\phantom{2-\alpha + \gamma((\sigma+1)-2(\tau-1))}\}
\end{aligned}
\begin{aligned}\zeta\ge
\max
\{&2-\alpha,\\
&2-\alpha + \gamma(\alpha-(\tau-1)),\\
&\phantom{2-\alpha + \gamma((\sigma+1)-2(\tau-1))}\}
\end{aligned}
\begin{aligned}\zeta\ge
\max
\{&2-\alpha,\\
&2-\alpha + \gamma(\alpha-(\tau-1)),\\
&2-\alpha + \gamma((\sigma+1)-2(\tau-1))\}
\end{aligned}
Cluster-size decay (Julia)
By joostjor
