based on the paper of prof. Dan Crisan et al., 2018, 
Imperial College, London

Introduction

Challenges in weather forcasting and climate change predictions

• measurement errors
• measurement uncertainty

Modeling:

due to:

• incomplete data
• incomplete theoretical knowledge

Data driven models

• values and uncertainty of future measures

Predict:

based on:

• input of measures and statistical anaysis of the initial data

Data assimilation: "in flight corrections" allows Numerical weather predictions

A stochastic framework for a data-driven model

• introduction of noise should preserve the fundalmental mathematical structure of the deterministic model
   
• Why consider the SALT equations:
  • not aiming to resolve the unresolved scales to predict their effects increasing the resolution
     
  • whereas, using the spatial correlation of the datas to model the effect of the uncertainty as spatially correlated stochastic transport

3D Euler SALT equations

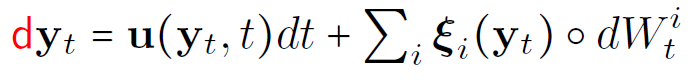
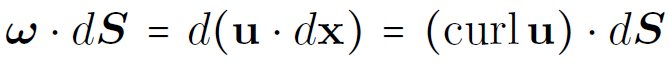
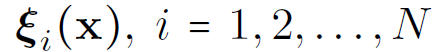
divergence free vector fields to be determined from the data

is the vorticity field

Emprical Orthogonal Functions (EOF)

Numerically (fine-coarse grid)

Uncertainty quantification (UQ) using SALT

• Fine grid Lagrangian trajectories (deterministic PDE)
   
• Coarse grid Lagrangian trajectories  (deterministic PDE -spatially filter velocity)
   
• Difference between fine-coarse grid trajectory on non-overlappling time intervals (velocity-velocity correlation tensors)
   
• Velocity-velocity correlation tensors substitute in SALT to perform UQ

2D Euler SALT equations on a square

2D Euler equations: deterministic

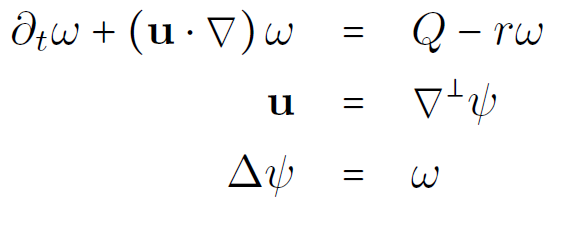
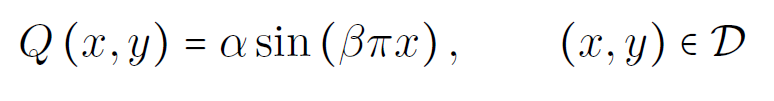
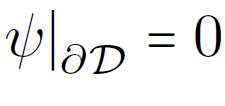
forcing

boundary condition

damping rate

Numerical scheme
 

• SPACE: Galerkin finite elements
   

• TIME: 3rd order Runge-Kutta

Bernsen et al. [2006]; Gottlieb [2005]

SPACE: Galerkin finite elements

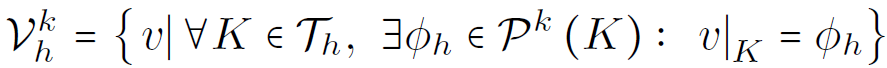
Discontinuous Galerkin for the vorticity equation

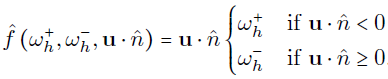
Continuous Galerkin for the elliptic equation

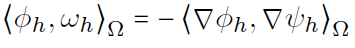
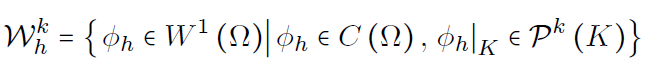
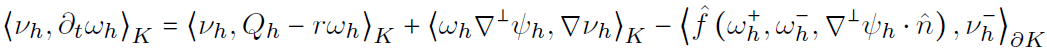
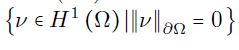
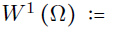
Energy conservation minus the source terms

Conserves the numerical
flux across neighbouring elements

u is continuous across the elements

TIME: 3rd order Runge-Kutta

Courant-Friedrich-Lewy (CFL) condition: C = 1/3

Δ := t_i+1 - t_i

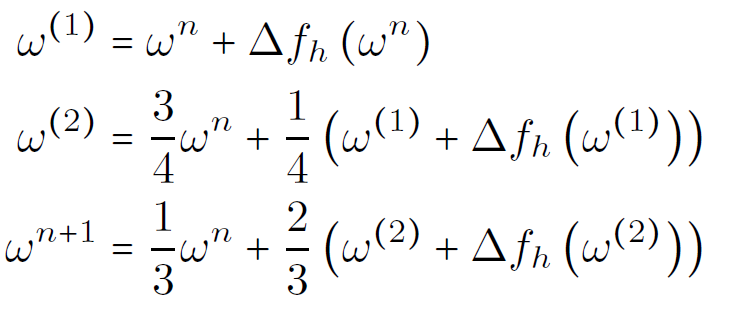
2D Euler equations: stochastic

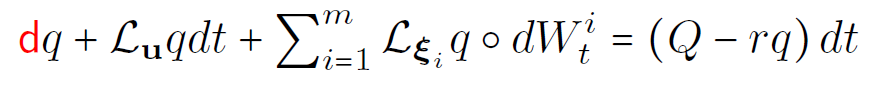
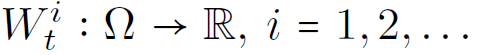
Lie derivative

Sequence of indepentent Brownian motions

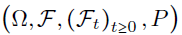
Filtered probability space

[Holm, 2015]

2D Euler equations: stochastic

eigenvectors of the velocity-velocity correlation tensor: divergence free

[Holm, 2015]

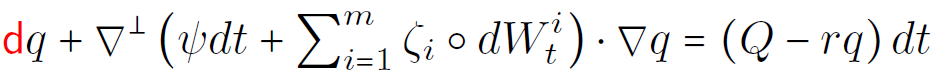
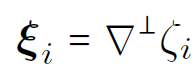
Transport velocity

Numerical scheme
 

• SPACE: Galerkin finite elements
   

• TIME: 3rd order Runge-Kutta

TIME: 3rd order Runge-Kutta

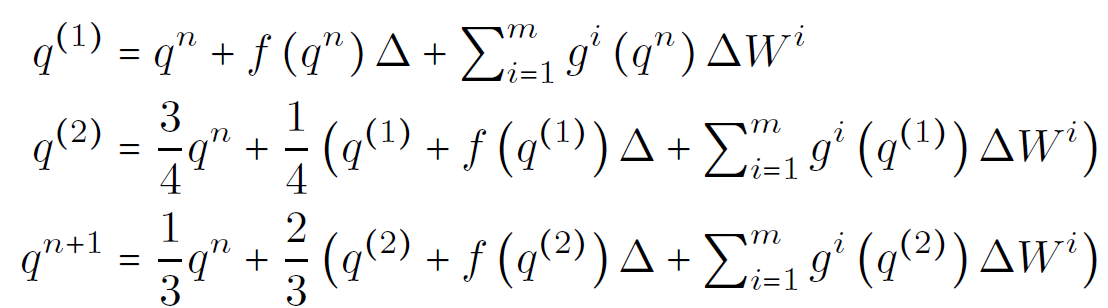
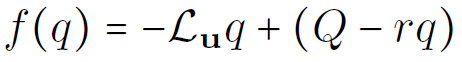
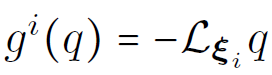
Combining SPACE-TIME

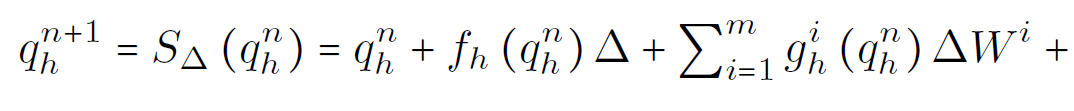
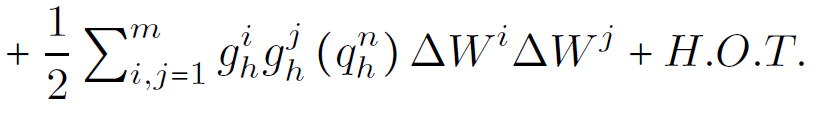
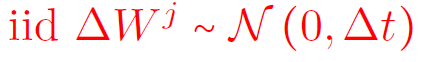
Consistency of the numerical method for the SPDE

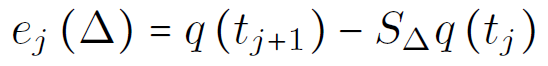
Local truncation error

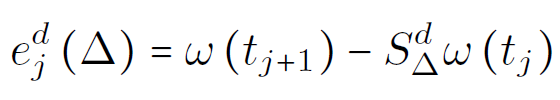
Local truncation error - deterministic

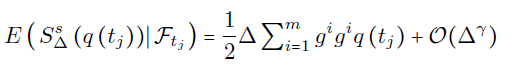
Def. For some γ>1, the discrete approximation operators S_Δ is called F-compatible  if S_Δ is F_tj+1 measurable and

for all j=0,...,n-1.

Consistency of the numerical method for the SPDE

Def. We say that the numerical scheme S_Δ  is consistent in mean square of order γ>1, w.r.t. the SPDE, if there exists a constant c independent on Δ ∈ (0,T], and for all ε>0 there exists 𝛿>0 such that for all 0<Δ<𝛿 and j=1,...,N:

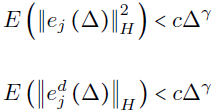
and S_Δ  is F-compatible.

Consistency of the numerical method for the SPDE

Thm. Assuming the SPDE well-posed and for all T>0 and sufficiently large p, we have

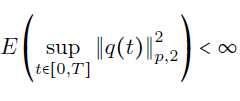
then the numerical schem S_Δ is consistent with γ=2.

[Crisan et al, 2018]

Calibration of the correlation eigenvectors

Assumptions in stochastic GFD

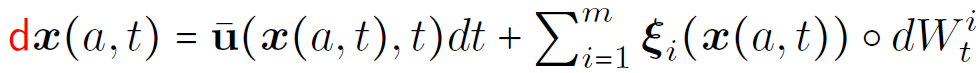
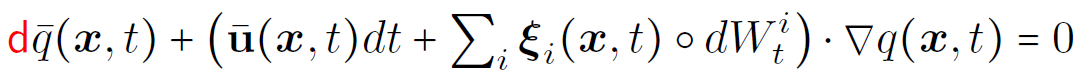
Averaged fluid particles equations of motion:

Eulerian stochastic QG equation

Estimation of the ξ

Deterministic unapproximated trajectories (fine grid):

Equations for ξ

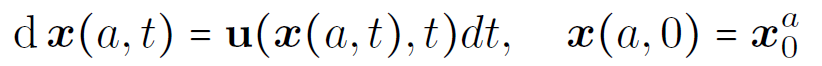
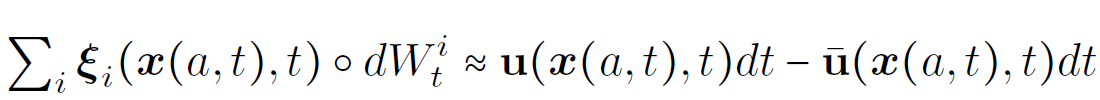
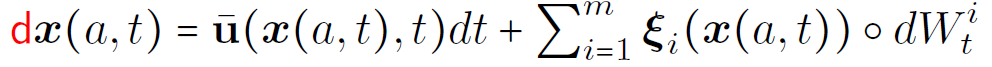
Stochastic trajectories (coarse grid):

Methodology

• Spin up a fine grid simulation from t = −T_spin to t = 0 (till some statistical equilibrium is reached)
   
• Record velocity time series from t = 0 to t = MΔt
   
• Define        as coarse grid points 

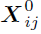
For each m=0,...,M-1

• Solve                                    for the initial data
  and u(x,t) solution of the fine grid simulation          

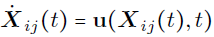
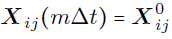
Methodology

• Compute              by spatially averaging u over the coarse grid
• Compute         by solving                           with the same initial condition
• Compute the difference
  which measures the error between the fine and coarse trajectory                                                           

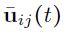
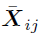
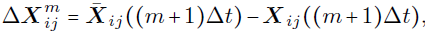
Finally, extract a basis for the noise minimizing:

N can be inferred by using EOFs

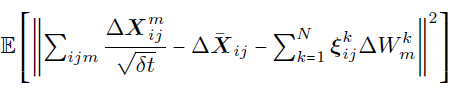
Numerical experiments for UQ

Initialization

• Solve deterministic PDE on a grid 512x512
   
• Coarse grain the solution to a grid 64x64 (thruth)
  • spatial average of the stream function
  • project it on the coarse grid
     
• The set of initial conditions at t0 is determined by letting the system to reach an energy equilibrium from an inital point at t_spin
   
• Time measured in ett = large eddy turnovers

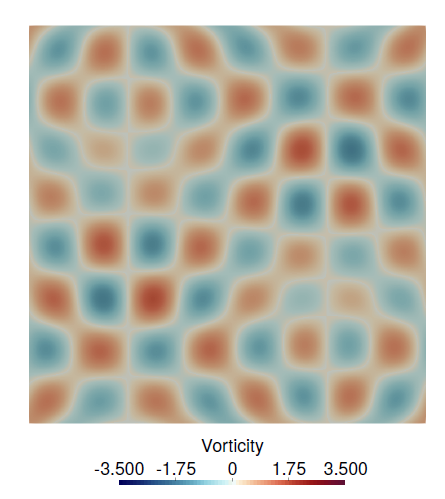
Initial vorticity at t_spin

Energy diagram

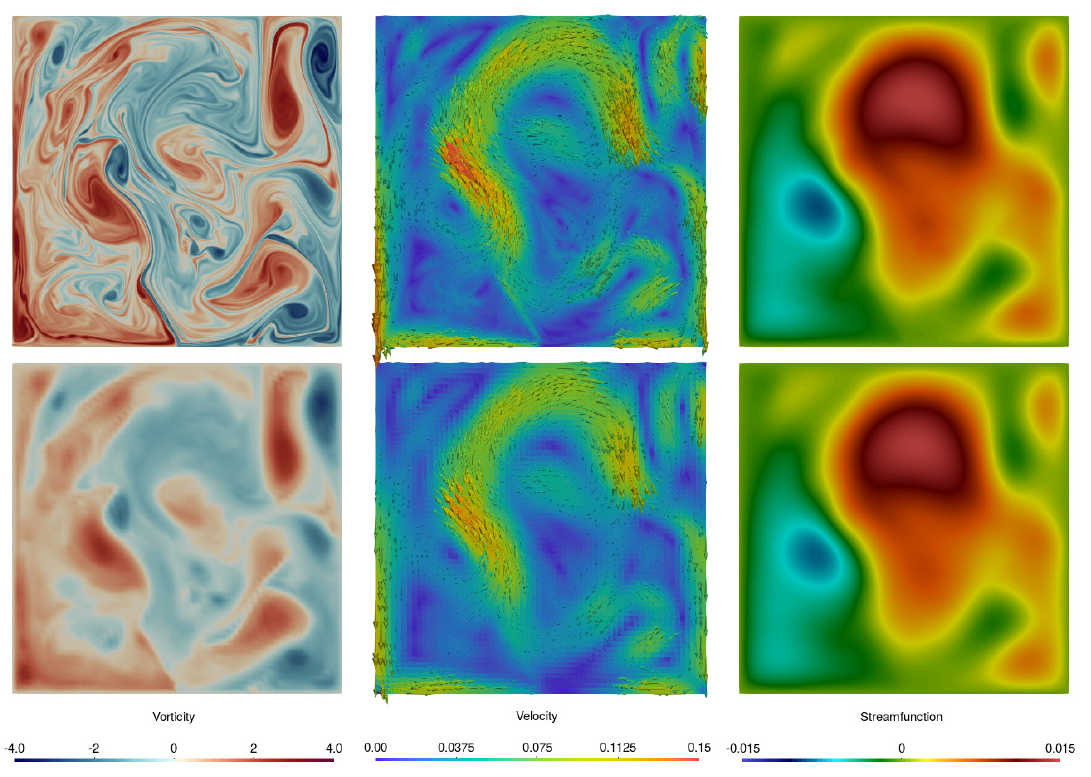
Vorticity

Velocity

Streamfunction

t = t0

Vorticity

Velocity

Streamfunction

t = t0 + 146

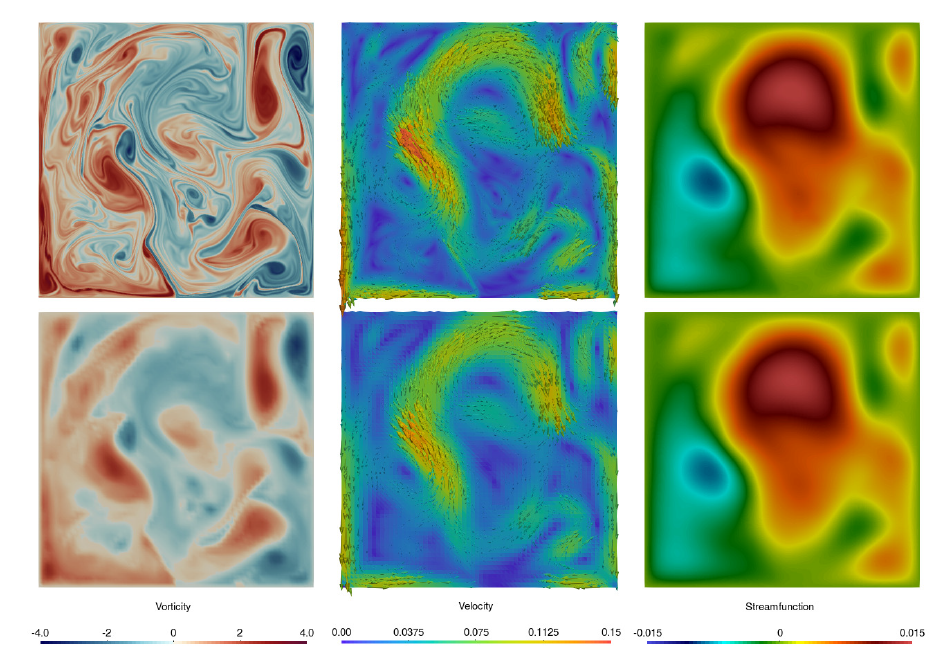
Lagrangian trajectories and estimating the correlation eigenvectors

• Compute the difference
  which measures the error between the fine and coarse trajectory                                                           

Finally, extract a basis for the noise minimizing:

N can be inferred by using EOFs

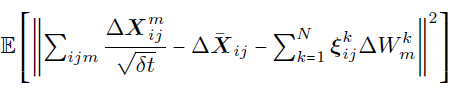
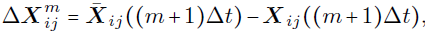
Uncertainty quantification test

• Substitute the computed ξ and simulate an ensemble of independent realisations of:
  
   
• Simulated 200 Lagrangian trajectories driven by the above equation, EOF capturing 90% of total variance
   
• Small time step: no significant deviations between the stochastic trajectories and the deterministic ones

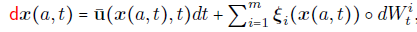
SPDE ensemble and SPDE initial conditions

• SPDE run on a 64x64 grid
   
• An ensemble of Np initial conditions for the SPDE are
  generated (each realization is called a particle)
   
• Goal when generating the initial conditions is to obtain an ensemble which contain particles that are "close"
  to the truth.
   
• Done with a deformation process solving for 1-2 ett the SDE:

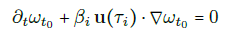
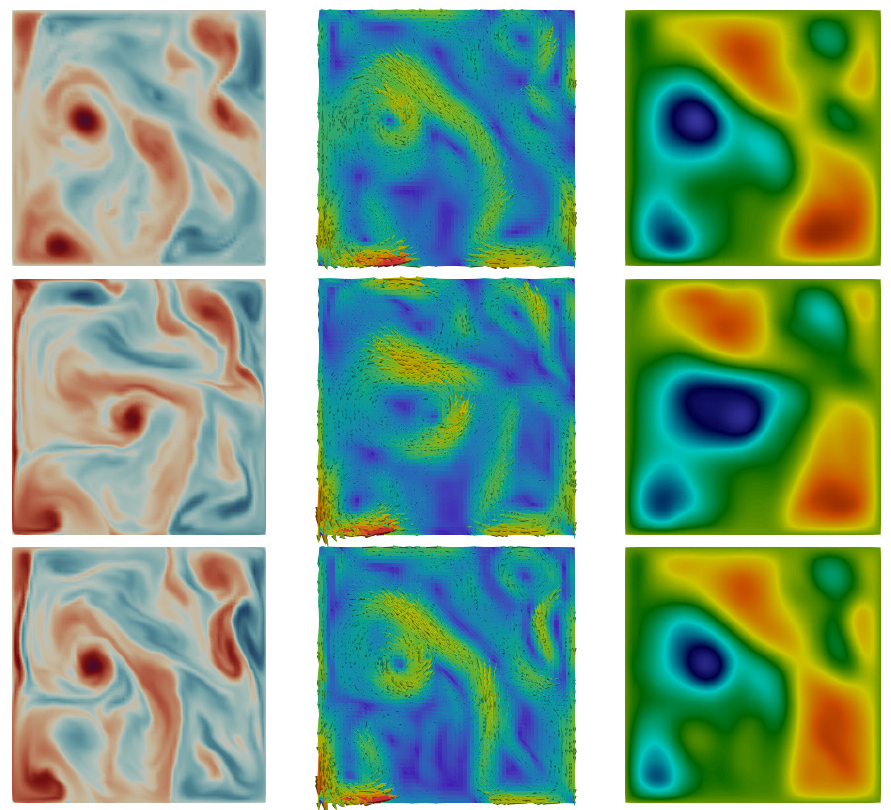
Vorticity

Velocity

Streamfunction

t = t0

Vorticity

Velocity

Streamfunction

t = t0 + 3

Vorticity

Velocity

Streamfunction

t = t0 + 5

SPDE uncertainty quantification

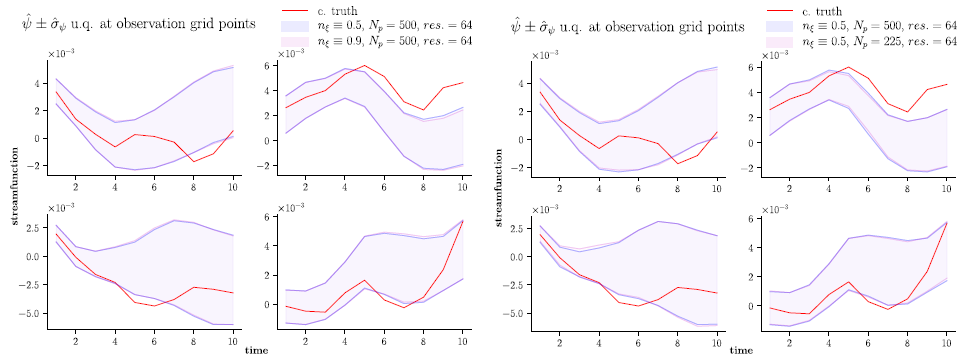
Uncertainty quanti cation plots comparing the truth with the ensemble one standard deviation region
about the ensemble mean for the streamfunction at four interior grid points of a 4 × 4 observation grid

Streamfunction

Uncertainty quanti cation plots comparing the truth with the ensemble one standard deviation region
about the ensemble mean for the streamfunction at four interior grid points of a 4 × 4 observation grid

Vorticity

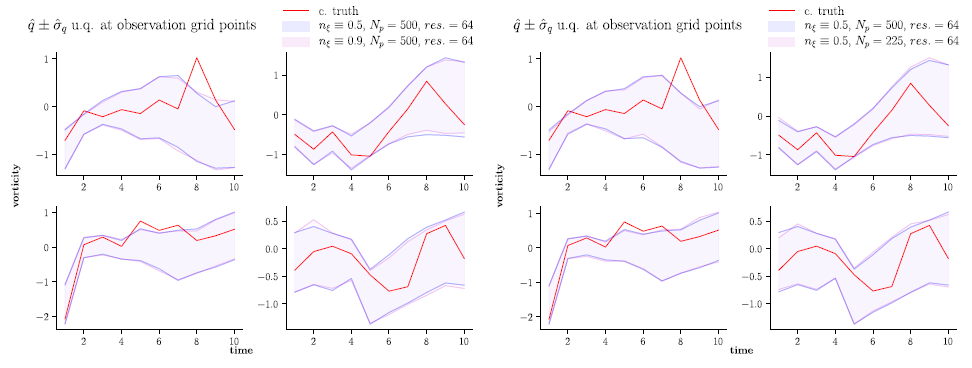
Uncertainty quanti cation plots comparing the truth with the ensemble one standard deviation region about the ensemble mean for the streamfunction at four interior grid points of a 4 × 4 observation grid

Streamfunction - different resolutions

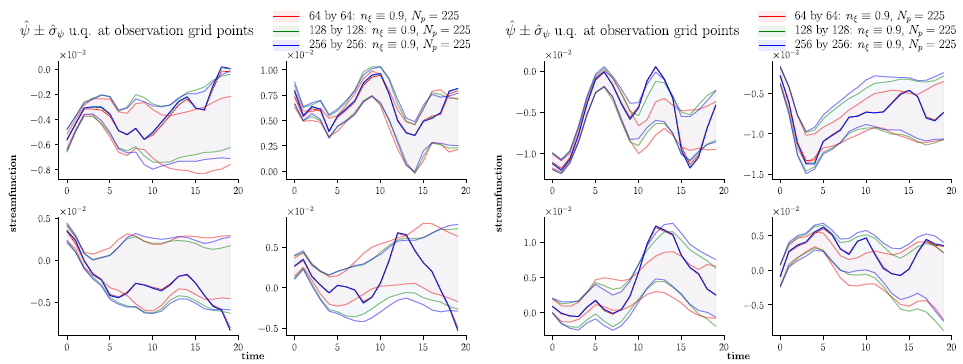
RMK: the coarse grid resolution gets re ned, the one
standard deviation region stays closer to the truth for longer time periods.

Uncertainty quanti cation plots comparing the truth with the ensemble one standard deviation region about the ensemble mean for the streamfunction at four interior grid points of a 4 × 4 observation grid

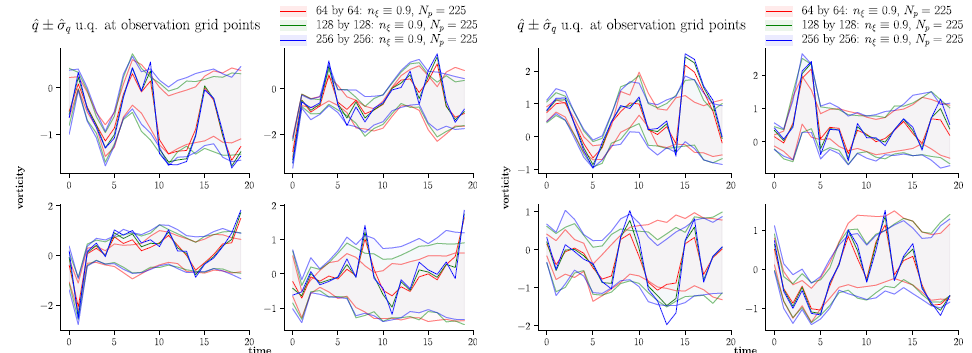
Vorticity - different resolutions

RMK: the coarse grid resolution gets re ned, the one
standard deviation region stays closer to the truth for longer time periods.

Conclusions

Conclusions

• New approach of data assimilation using the SALT equations: geometric mechanics-variational derivation
   
• Stable numerical method scheme for both stochastic and deterministic models
   
• UQ: the uncertainty decreases as the grid becomes more refined, and the fidelity to the true solution increases as the size of the ensemble increases
   
• Q: applying a geometric integrator would affect the UQ?

Thanks for your attention